Der Nenner des ersten Terms lässt sich
faktorisieren zu ( x + 3 ) * ( x -2 )
und wird somit null für
x = -3
und
x = 2
Der Nenner des zweiten Terms lässt sich
als ( x -3 )^2 schreiben
und wird somit null für
x = 3
D = ℝ \ [ -3, 2, 3 ]
Der Zähler des 2.Terms läßt sich schreiben als
( 2x - 6)^2
[ 2 * ( x -3 ) ]^2
4 * ( x -3 ) ^2
Der 2.Bruch lautet
4 * ( x -3 ) ^2 / ( x -3 ) ^2
Für lim x −> 3 darf gekürzt werden zu
4
Im ersten Term kann leider nichts gekürzt
werden.
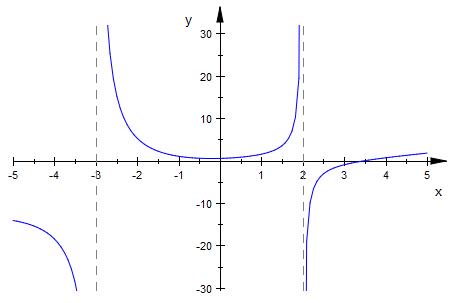
Bei x = -3 und x = 2 kann nicht stetig fortgesetzt werden.