Hallo Lolo,
A 7)
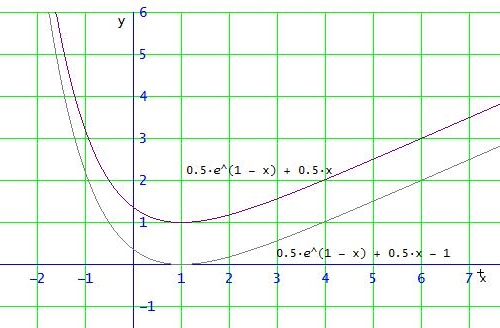
fa(x) = 0.5·e^{1 - x} + 0.5·x + a ergibt sich aus f(x) = 0.5·e^{1 - x} + 0.5·x durch Verschiebung um a in y-Richtung.
Rechne aus, für welchen Wert f(x) = 0.5·e^{1 - x} + 0.5·x die x-Achse berührt:
f '(x) = 0 ⇔ - 1/2 * e^{1 - x} + 1/2 = 0 ⇔ x = 1
An dieser Stelle hat f den Wert f(1) = 1 → Extrempunkt (1|1)
Die Funktion f muss also um a = - 1 (nach unten verschoben werden) damit fa(1) = 0 wird.
A8)
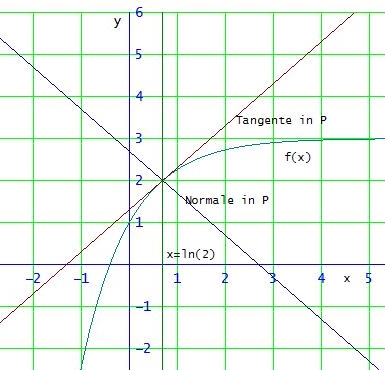
a) f '(x) = 2·e-x = 0 hat keine Lösung
b) die 2. WH y = -x hat die Steigung -1
Normalensteigung = -1 / f '(x) , weil die Normale senkrecht auf der Tangente steht.
Löse die Gleichung -1 / f '(x) = -1 , also f '(x) = 1 ⇔ 2·e-x = 1 → xp = ln(2)
mit f( ln(2) ) = 2 hast du dann den gesuchten Punkt P(ln(2) | 2)
Gruß Wolfgang