Integralrechnung (Fläche) - Ufer/Kanal Aufgabe

Question

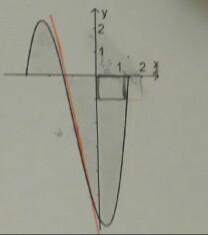
ich habe eine Aufgabe bei der ich nicht ganz weiter komme. Ich bin ein mittelmäßigee Schüler und komme deshalb nicht allzu schnell mit im Unterricht.

Im Anhang sehen Sie die Aufgabe.

Ausgangsfunktion: f(x)=x^3+3x^2-2x-6

Bei Nr. d) vermute ich mal, dass ich irgendwas mit Extrempunkten machen muss? Aber verstehe nicht wirjlich den Sachverhalt und weiß auch nicht wie ich vorgehen soll..

Bei Nr. e) weiß ich (glaube ich eher gesagt), dass ich eine Flächenberechnung mit dem Integral in einem Intervall vornehmen muss und dann im Anschluss das Volumen ausrechnen muss. Weiß aber nicht wie ich vorgehehn soll, könnten Sie mir hier bitte zumindest. Ansätze geben mit eventuell Zwischenschritten.

Also d) weiß ich überhaupt gar nicht wie..

Und bei e) weiß ich vielleicht etwas aber auch nicht wie ich angehen soll

Ich habe bereits diese Aufgabe in einem anderen Post gestellt aber nur als Kommentar und jetzt halt als separate Frage zur besseren Übersicht auch.

Danke

Comments

Bei d) machst du eine Betrachtung der Extrempunkte. Die x-Achse ist ja die Wasseroberfläche und du sollst ja die maximale Tiefe ausrechnen, heißt du brauchst den Tiefpunkt (siehst du ja ander Skizze) und du sollst den ochpunkt ausrechnen, da du ja die maximale Höhe brauchst. Das siehst du auch an der Skizze.

Bei e) Musst du das Integral im Intervall [$$ \sqrt { -2 } |  \sqrt { 2 } $$] berechnen.

---

$$ \int_{-\sqrt {2}}^{\sqrt { 2 }}(x3+3x2-2x-6)dx =| [\frac { 1}{ 4 }{ x }^{ 4 } + { x }^{ 3 } - { x }^{ 2 }-6x]|= |-11,31| = 11,31FE$$

---

Danke den ersten Teil deiner Antwort habe ich verstanden, aber du meinst beim 2. Teil aufgabe d) und nicht e) oder, weil das gehört ja beides zu d)?

Und was soll ich bei e) dann machen?und die 15 Meter da?

---

Nein ich meine schon e), da du ja gegeben hast, dass das der Kanal im oben angegeben Intervall verläuft. Und diese sind daher auch deine Grenzen für dein Integral.

---

Ah ok, und was mache ich dann mit den 15metern bei e)?

---

Ah ich habs.

Die Querschnitrafláche dann mal 15 multiplizieren oder?

Macht dann 169.5 m^3 oder?

---

Ja hätte ich jetzt auch so gemacht. (Angaben ohne Gewähr :D)

Answer 1

Ich kann die Rechnung bestätigen

d)

f(x) = x^3 + 3·x^2 - 2·x - 6

f'(x) = 3·x^2 + 6·x - 2 = 0 --> x = -2.291 ∨ x = 0.2910

f(-2.291) = 2.303 m --> maximale Höhe der Uferböschung

f(0.2910) = -6.303 m --> maximale Tiefe des Kanals

e)

f(x) = x^3 + 3·x^2 - 2·x - 6 = 0 --> x = ± √2 ∨ x = -3

∫(x^3 + 3·x^2 - 2·x - 6, x, - √2, √2) = - 8·√2 = -11.31 m²

V = G·h = 11.31·15 = 169.7 m³

Rundungsdifferenzen sind ganz ok.