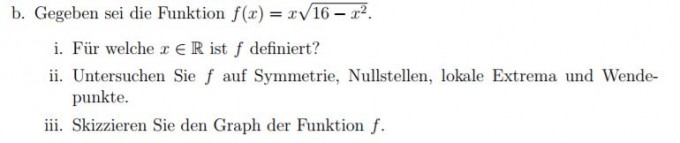Hey:)
Also meine Ergebnisse lauten:
i. D={x ∈ R | -4<= x <=4}
ii. Nullstellen
Term gleich null setzen, ergibt: x1=0, x2=4, x3=-4.
Extrempunkte:
Erste Ableitung:
√(16-x^2) - (x^2 /(√(16-x^ 2 )
ergeibt √8 und -√8.
Nun, wollte ich die zweite Ableitung berechnen.
die wäre doch
-x/(√(16-x^2)) -( x^3 / (16-x^2)3/2)
Dann ergebe bei Wurzel 8 einen Hochpunkt und bei -Wurzel 8 Tiefpunkt-
Wendepunkt.
Zweite Ableitung null setzen und schauen, ob dritte Ableitung ungleich null.
Symmetrie:
Und es ist punktsymmetrisch, weil f(-x)=-f(x)