Bestimme die farbige Fläche f(x)= 1/6 x^2 - x + 3/2. g(x) = -1/9 x^2 + 2/3 x+ 3/2. im Intervall [ 0; 8,5 ] .

Question

bestimme die farbig unterlegte fläche zwischen den Funktionen

f(x)= 1/6 x^2 - x + 3/2.   g(x) = -1/9 x^2 + 2/3 x+ 3/2.      im Intervall [ 0; 8,5 ] .

Comments

Hat dein Intervall 3 Grenzen? Wie meinst du das?

---

ververstehe die aufgabe nicht  bitte lösungsweg angaben aufgane 3

---

Aha. Da war ein Strichpunkt im Intervall. Ich ändere das. Das Bild gehört aber zur Aufgabe vorher?

---

ja  verstehe die aufgabe nicht

Answer 1

d(x) = (1/6·x^2 - x + 3/2) - (-1/9·x^2 + 2/3·x + 3/2) = 5/18·x^2 - 5/3·x

D(x) = 5/54·x^3 - 5/6·x^2

Ist dann das Intervall [0.8 ; 5] gemeint ? Dann wäre es

D(5) - D(0.8) = ...

Comments

als Lösung soll A= 3,34 FE raus kommen  wie kommen die auf die Lösung                bitte rechnenweg angeben

---

Du hast vermutlich eh nicht die komplette Aufgabe fotografiert, denn dort ist keine Skizze wo man die farbig unterlegte Fläche sieht.

∫ (0 bis 8.5) (5/18·x^2 - 5/3·x) dx = -3.345 FE

Dei Flächenbilanz im Intervall [0 ; 8.5] beträgt 3.3345 FE. Das ist nicht die Fläche im Intervall !

Die Fläche hätte tatsächlich einen Flächeninhalt von ca. 16.66 FE

Solltet Ihr die Lösung vom Lehrer haben bitte nochmals um eine nähere Erläuterung und weise auf einen Unterschied zwischen Flächenbilanz und Fläche hin.

Answer 2

Die farbige Fläche ist nicht abgebildet worden. Ich gehe daher davon aus, dass die farbige Fläche von den Graphen der Funktionen g und f sowie von der Geraden mit der Gleichung x=8,5 gebildet wird.

Berechne die Differenzfunktion g(x)-f(x)=5/18·x·(6-x). Ihre Nullstellen sind x=0 und x=6. Bilde das Integral der Differenzfunktion in der Grenzen von 0 bis 6 und das Integral der Differenzfunktion in der Grenzen von 6 bis 8,5 und addiere die Beträge.

Answer 3

Hallo VKK,

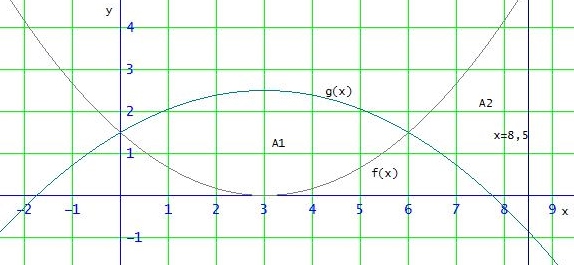
Den Flächeninhalt der Fläche zwischen 2 Graphen kann man mit der Differenzenfunktion d(x) = f(x) - g(x) ausrechnen:

d(x) = f(x) - g(x)  =  (1/6·x^2 - x + 3/2) - (- 1/9·x^2 + 2/3·x + 3/2)

        =  5/18 · (x² - 6x)  = 5/18 · x · (x - 6)  

Da  f und g sich im Intervall  [0 ; 8,5]  in x=0 und x=6   schneiden, muss man für die Gesamtfläche die Teilflächen A1 und A2 ausrechnen und addieren:

A = |  ₀∫⁶   5/18 · (x² - 6x)    dx |  +   | ₆∫^8,5   5/18 · (x² - 6x)  dx |

        Der 2. Betrag könnte entfallen, weil dort f(x) oberhalb von g(x) verläuft.

A  =  | [ 5·x^3/54 - 5·x^2/6 ]₀⁶ | +  [ 5·x^3/54 - 5·x^2/6 ]₆^8,5

     =  ...  ≈   |-10| +  6,655   ≈ 16,655  [FE]

Gruß Wolfgang