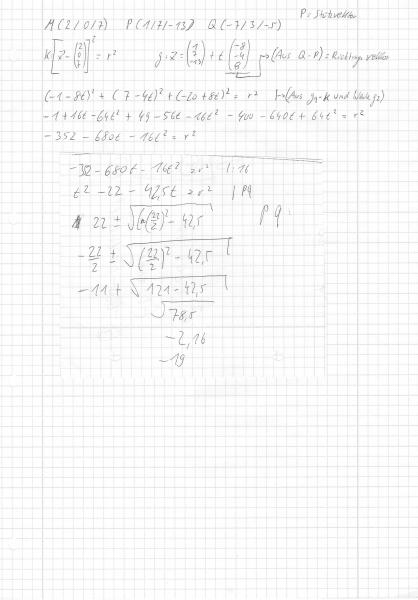Wie ist der Radius zu wählen, damit die Gerade die Kugel berührt?

Question

hänge momentan an einer Mathe Aufgabe, dessen Typ von Aufgabe wir heute das erste Mal bekommen haben.

Die Fragestellung lautet:  Wie ist der Radius der Kugel um M(2/-1/5) zu wählen, damit die Gerade g:x:(3/-9/10)+t                                                (1/4/-1) die Kugel berührt?

Ich habe, wie auf dem Bild unten zu sehen ist, zuerst die Kugelgleichung als auch den Richtungsvektor bestimmt. Daraufhin die quadratische Gleichung aufgeschrieben. 

Nun habe ich erstmal auf einen anderen Zettel versucht mit der PQ-Formel weiter zu rechnen. Jedoch ist das Ergebnis glaube ich nicht richtig. Wie hätte ich weiter rechnen müssen bzw. ist das hervorgegangene richtig?

Bin echt kein Mathe Genie aber in zwei Wochen schreiben wir unsere Klausur und die muss unbedingt gut werden. Deshalb würde ich mich für hilfreiche Antworten bzw. mit der weiterrechnung mich sehr freuen :)

und weiterhin einen angenehmen Tag.

 

Answer 1

Viel zu kompliziert. Du sollst doch nur den Radius berechnen - wozu benötigst du da die Kugelgleichung?

Wenn eine Gerade eine Kugel berührt, dann steht sie senkrecht auf dem Kugelradius. Der Radius ist dann also der Abstand der Geraden vom Mittelpunkt der Kugel.   

Bestimme daher einfach den Abstand des gegebenen Kugelmittelpunktes von der gegebenen Geraden. Dieser Abstand ist gleich dem gesuchten Kugelradius. 

Wie man den Abstand eines Punktes von einer Geraden bestimmt, kannst du z.B. hier nachlesen:  

http://www.frustfrei-lernen.de/mathematik/abstand-punkt-gerade.html