Konvergenzradius bestimmen Potenzreihe: Summe (n^4 - 4n^3)/(n^3 + n^2) x^n

Question

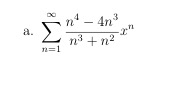
Hey:)

Ich soll den Konvergenzradius dieser Potenzreihe bestimmen.

Und es gibt ja die Formel 1/ lim n->unendlcih n-te√|an|.

Und jetzt dachte ich, dass ich einfach jetzt die n-te Wurzel ziehe also je ein n aus jedem Teilterm nur weiß ich nicht, ob ich das wirklich Sinn macht. 

Und wegen dem x^n ist es ja nur noch x. Aber letztendlich will ich sagen, dass ich einfach nicht weiter weiß ...

Comments

Divergiert die Reihe?

---

Wie sieht denn deine Rechnung aus? 

---

Hab n^3 ausgeklammert:

Und dann steht da n-4/ (1+1/n) und dann geht es gegen unendlich und damit divergiert 

---

Passt das so?:)

---

Für große n gilt 

(n^4-4n^3)/(n^3+n^2)≈n^4/n^3=n

Es reicht also die Reihe über n*x^n zu betrachten, damit lässt es sich leichter rechnen. 

Im übrigen kannst du hier auch folgende Formel verwenden:

$$ r=\lim_{n\to\infty}|\frac {  { a }_{ n }}{  { a }_{ n+1 }}| $$

Answer 1

Für große n gilt 

(n^4-4n^3)/(n^3+n^2)≈n^4/n^3=n

Es reicht also die Reihe über n*x^n zu betrachten, damit lässt es sich leichter rechnen. 

Im übrigen kannst du hier auch folgende Formel verwenden:

$$ r=\lim_{n\to\infty}|\frac {  { a }_{ n }}{  { a }_{ n+1 }}| $$

Gibt als Ergebnis dann r=1.

Comments

Muss ich da noch die Randbereiche überprüfen?

---

Da divergiert es doch oder?

Für beide Randbereiche, da

1* n für n gegen unendlich 

-1 * n gegen unendlich