Würfel Knobelaufgabe

Question

Ich bin auf ein interessantes Problem gestoßen:

Stell dir vor du würfelst mit vier sechseitigen Würfeln. Du addierst die drei höchsten Werte zusammen und lässt den niedrigsten Wert außen vor. 
( Bsp. 5 - 4 -1 - 6, die drei höchsten Werte ergeben in diesem Fall 15 )

Was wäre der durchschnittliche Endwert, der aus diesem Verfahren heraus resultiert ?

Answer 1

TabKalk

Baue 4 Würfel:

A1:D1=REST(GANZZAHL((ZEILE()-1)/POTENZ(6;(SPALTE()-1)));6)+1

F1=SUMME(A1:D1)-MIN(A1:D1)

A1:F1 Kopieren bis 6^4 = A1296

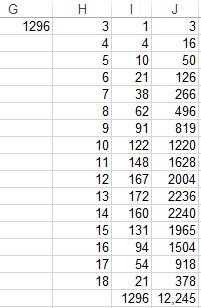
H1=3...H16=18

I1:I16=ZÄHLENWENN($F$1:$F$1296;H1)

J1=H1*I1 ... J16==H16*I16

 

Vielleicht findet jemand eine geschlossene Lösung - das wäre erstmal eine Antwort auf die Fage...

Comments

Hallo wächter,

ich habe das gleiche Ergebnis. Der exakte Wert ist \(15869/1296\) - ... gefühlt ist die Zahl zu krumm für eine geschlossene Lösung.

---

Hallo Werner,

ja, dachte ich mir auch - wegen Min abziehen - aber beweise das mal ;-)?

Zum Glück gibbet ja Excel und Co und wir sind jetzt schon zu zweit.....

uups:Fage = Frage