Max Gewinn Fabrikant Kf und kv

Question

Ein Fabrikant kann von einer Ware bei einem Preis von 81 GE 1370 Stück, bei einem Preis von 177 GE aber nur 810 Stück absetzen. Dem Fabrikanten entstehen Fixkosten von 27800 GE und zusätzlich pro Stück Kosten von 10 GE. Berechnen Sie den Gewinn, den der Fabrikant maximal erzielen kann.

a. 63455.85
b. 60942.22
c. 108625.03
d. 201075.03
e. 188526.95

Die Cx ist ja bereits gegeben: 10x + 27800
Dann müsste man aus der D(p) die E(p) machen oder?

Answer 1

Du verwendest hier Begriffe (Kf, kv, Cx, D(p), E(p)), die vielleicht in deiner Klasse oder in deinem Lehrbuch eingeführt sind, mit denen der Rest der Welt aber nichts anfangen kann.

Falls die Nachfragefunktion (x Menge, y Preis) linear ist (warum sollte sie), dann folgt aus den beiden Punkten (1370, 81) und (810, 177) die Funktion Preis =  -6/35 Menge + 315.857

Der Gewinn ist dann Erlös - Kosten = Preis * Menge - Kosten = (-6/35 * Menge + 315.857) * Menge - (10 * Menge + 27800)

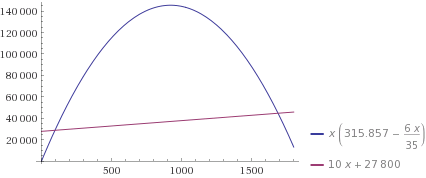
Ich komme auf ein Gewinnmaximum bei 892 Stück und Antwort (c) als richtige Lösung.

Comments

vielen Dank, hab alles verstanden!

---

Man könnte sich noch fragen, warum die Nachfragemenge linear vom Preis abhängen soll, inklusive der in dieser Aufgabenstellung implizierten Behauptung, dass 1842 Stück genommen werden, wenn es gratis verteilt wird. Dann hat man mindestens zwei Alternativen: Entweder markiert man die aufgeweckte Schülerin und stellt den Mathelehrer zur Rede über diese unplausible Annahme im Modell der Aufgabenstellung. Wenn man dabei den richtigen Zeitpunkt und die richtige Tonlage wählt (und den richtigen Lehrer hat), kann das gutgehen. Oder man gibt sich weise und erkennt, dass hier nicht ein Modell vermittelt werden soll, sondern Rechenfähigkeiten, und man das Modell an die zu trainierende Technik angepasst hat. Dahinter steckt die löbliche Absicht, die Schüler mit anwendungsorientierten Aufgaben motivieren zu wollen.

Answer 2

p(x) = (81 - 177)/(1370 - 810)·(x - 810) + 177 = 2211/7 - 6/35·x

G(x) = x·(2211/7 - 6/35·x) - (27800 + 10x) = - 6/35·x^2 + 2141/7·x - 27800

G'(x) = 2141/7 - 12/35·x = 0 --> x = 892.1 ME

G(892.1) = - 6/35·892.1^2 + 2141/7·892.1 - 27800 = 108625 GE

c) sollte also richtig sein.