Umkehrfunktion bilden von f(x)=3x*(-1+ln(x))

Question

ich sitze fest und benötige die Umkehrfunktion von

 f(x)=3x*(-1+ln(x))

und benötige eigentlich Hilfe :D

Answer 1

1. Schritt: Kontrollieren, ob und wie eine Fallunterscheidung nötig ist.

 ~plot~ 3x*(-1+ln(x));x=1 ~plot~ 

Du kannst f(x) entweder im Bereich 0≤x≤1 oder im Bereich x≥ 1 umkehren.

Wenn du dich entschieden hast, musst du 

y = 3x*(-1+ln(x)) 

nach x auflösen. 

Das ist mit den üblichen Rechenoperationen aber nicht möglich! 

Wozu brauchst du die Umkehrfunktion? 

Beim Umweg über die komplexen Zahlen, kommen sogar noch weitere Fälle dazu. Aber eben, auflösen nach x kannst du deine Gleichung doch nicht. 

https://www.wolframalpha.com/input/?i=3x*(-1%2Bln(x)) 

Answer 2

Auch wenn die "beste Antwort" schon vergeben ist, hier noch 2 Hinweise:

1. wenn nur grafisch gespiegelt werden soll, lässt sich das am besten per "Parameterdarstellung" tun

x(t) und y(t) sind dann einfach zu tauschen -> man braucht dann keine Fallunterscheidung

2. weil hier mehrfach geantwortet wurde "Umkehrfunktion explizit nicht möglich":

die Inverse (Umkehrfunktion) zu f(x)=3x*(-1+ln(x))   oberhalb x>1 lautet:

x/(3*LambertW(x/(3*e)))

siehe http://www.lamprechts.de/gerd/LambertW-Beispiele.html

grafisch: https://www.wolframalpha.com/input/?i=plot+x%2F(3*LambertW(x%2F(3*e))),x%3D-3...2

Auch wenn LambertW(x) kein Schulstoff ist, so gehört sie doch zu den

https://de.wikipedia.org/wiki/Elementare_Funktion

Answer 3

Hallo JB,

f(x) = 3x * (-1+ln(x))    D = ℝ⁺    (ich gehe von der Grundmenge ℝ aus!) 

ist wegen

f '(x) = 3·LN(x)    negativ in  0 in ] 0 ; 1 [  und  positiv  und  in ] 1 ; ∞ [ 

in  ] 0 ; 1 ]  streng monoton fallend  und  in  [ 1 ; ∞ [  streng monoton steigend

also nicht injektiv in ℝ⁺.

Es gibt deshalb  ( f(1) = -3 )  nur Umkehrfunktionen g_i  bei eingeschränktem Definitionsbereich für f:

f₁:  [ 1 ; ∞ [    →    [ - 3 ; ∞ [   und   f₂:  ] 0 ; 1 ] →  [ - 3 ; ∞ [  

g₁: [ - 3 ; ∞ [   →   [ 1 ; ∞ [    und   g₂: [ - 3 ; ∞ [  →  ] 0 ; 1 ]  

Zur Berechnung der Funktionsvorschriften von g_i :

y =  3x * (-1 + ln(x)) 

Variablennamen vertauschen:

x = 3y * (-1 + ln(y)) 

Diese Gleichung müsste man jetzt nach y auflösen, was mit "normalen Mitteln" aber wohl nicht explizit möglich ist. 

Die  Graphen  der beiden Umkehrfunktionen g_i erhält man jeweils durch Spiegelung der Graphen der zugehörigen Funktion f_i an der 1. Winkelhalbierenden:

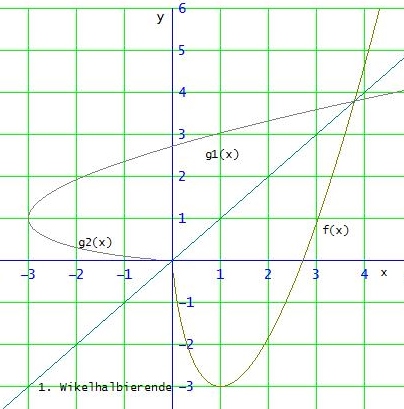
Gruß Wolfgang