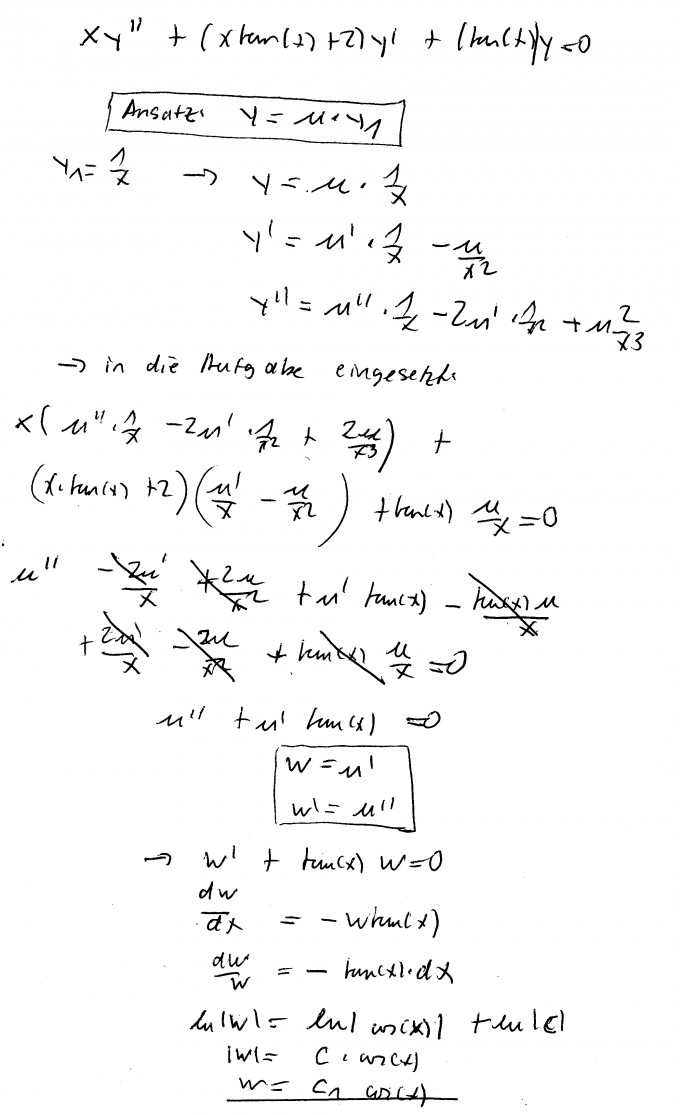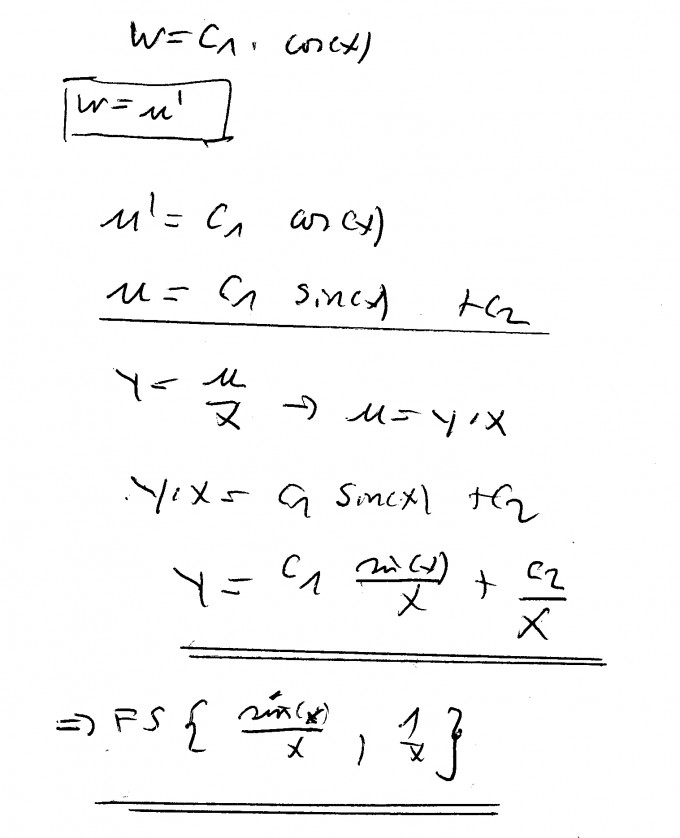\( xy'' + (x \tan(x) + 2)y' + ( \tan(x) ) y = 0 \)
Ansatz: y = u · y_{1}
\( y_{1} = \frac{1}{x} \)
\( y = u · \frac{1}{x} \\ y' = u' · \frac{1}{x} - \frac{u}{x^2} \\ y'' = u'' · \frac{1}{x} - 2u' · \frac{1}{x^2} + u \frac{2}{x^3} \)
In die Aufgabe eingesetzt:
\( x · ( u'' · \frac{1}{x} - 2u' · \frac{1}{x^2} + u \frac{2}{x^3} ) + (x \tan(x) + 2) \cdot (u' · \frac{1}{x} - \frac{u}{x^2}) + ( \tan(x) ) \frac{u}{x} = 0 \)

\( u'' + u' \tan(x) = 0 \)
\( w = u' \\ w' = u'' \)
\( w' + \tan(x) w = 0 \\ \frac{dw}{dx} = -w \tan(x) \\ \frac{dw}{w} - \tan(x) · dx \\ ln |q| = ln | cos(x) | + ln | c | \\ |w| = c·\cos(x) \\ w = c_{1} · cos(x) \)
\( w = c_{1} \cdot \cos(x) \\ w = u' \)
\( \underline{ u' = c_{1} \cdot \cos(x) \\ u = c_{1} · \sin(x) + c_{2} } \)
\( y = \frac{u}{x} \rightarrow u = y·x \\ y·x = c_{1} \sin(x) + c_{2} \\ y = c_{1} \frac{\sin(x)}{x} + \frac{c_{2}}{x} \\ \rightarrow FS \{ \frac{(sin(x)}{x}, \frac{1}{x} \}\)