Leider fehlt auch hier wieder die Angabe der Klassenstufe, denn natürlich gibt es exakte Lösungsformeln, die bei Gleichungen 3. Grades auch alle 3 Lösungen ausgeben:
Cardanische Formeln & PQRST-Formel:
http://www.lamprechts.de/gerd/php/gleichung-6-grades.php
rechnet es vor:
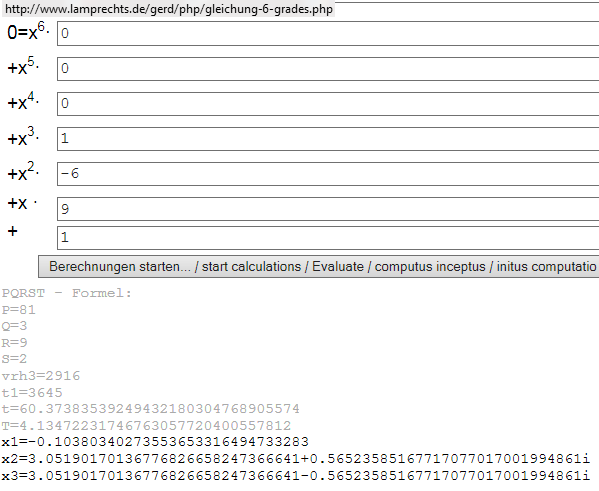
In der Schule kommt so etwas aber nicht vor! Selbst komplexe Lösungen nicht. Da wollen die Lehrer entweder:
Raten (und stellen nur Fragen nach glatten Lösungen), oder Newton-V. oder https://de.wikipedia.org/wiki/Bisektion
Für das exakte Ergebnis interessieren sich nicht mal Studenten im 1. Semester:
x
1= 2 - (3/2 - sqrt(5)/2)^{1/3} - (3/2 + sqrt(5)/2)^{1/3}