Simpson-Paradoxon - Mit welcher Wahrscheinlichkeit handelt es sich um ein blaues Taxi?

Question

ich habe folgende Aufgabe und weiß nicht so richtig, wie ich beginnen soll, diese zu lösen:

Ein Zeuge hat einen Unfall mit einem Taxi beobachtet, dessen Fahrer jedoch nicht anhielt, sondern die Fahrt fortsetzte. Der Zeuge gibt an, dass das Taxi eine blaue Farbe hatte. Die Zuverlässigkeit des Zeugen beträgt 80%, d. h. seine Aussagen sind erfahrungsgemäß in 80% der Fälle zutreffend. In der Stadt gibt es 180 gelbe und nur 20 blaue Taxis. Mit welcher Wahrscheinlichkeit sollte die Polizei davon ausgehen, dass es sich um ein blaues Taxi gehandelt hat?

Habt ihr einen Rat, wie ich beginnen soll?

Ich habe schon versucht so eine Tabelle für die Übersicht zu erstellen... eine Spalte wäre ja gelbe Taxis und eine Spalte blaue Taxis, aber was nehme ich für die Zeilen?

Für eure Hilfe bin ich sehr dankbar.



Alex

Comments

Zuerst solltest du dir überlegen, mit welcher Wahrscheinlichkeit ein blaues Taxi unabhängig vom Zeugen beteiligt war.

Answer 1

Hallo Alex, 

ich denke, Dein Ansatz ist sehr gut.

Ich würde die Vierfelder-Tafel so erstellen:

 

                                                Taxi gelb                            Taxi blau

Aussage richtig                      0,72                                       0,08                      0,8

Aussage falsch                      0,18                                       0,02                      0,2

                                               180/200                                 20/200                     1

 

Die roten Werte waren gegeben, die Werte in der Tafel ergeben sich durch Multiplikation mit den Randwahrscheinlichkeiten (wegen der Unabhängigkeit der beiden Ereignisse).

 

Allerdings hat mich sowohl die Zeilenbeschriftung als auch die anschließende Auswertung vor Probleme gestellt, weshalb es auch voneinander abweichende Lösungen gab. 

 

Übersichtlicher ist hier vielleicht ein Baumdiagramm wie folgendes: 

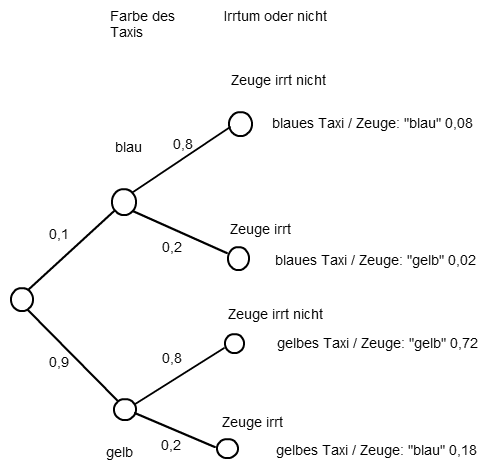
Jetzt sieht man recht schön, dass die Wahrscheinlichkeit dafür, dass der Zeuge "blau" aussagt und das Taxi tatsächlich blau war, 0,08 beträgt, also 8%.

Aber die Wahrscheinlichkeit dafür, dass der Zeuge "blau" aussagt und das Taxi in Wirklichkeit gelb war, beträgt

0,18, also 18%.

Dann ist die Wahrscheinlichkeit, dass das Taxi tatsächlich blau war, wenn der Zeuge dies ausgesagt hat:

8% / (8% + 18%) = 8% / 26% = 4/13% ≈ 30,8%

Diese korrekte Antwort hat der Mathecoach schon gestern gegeben!

 

Besten Gruß

Comments

danke für deine Antwort und das Baumdiagramm.

Ich habe noch eine Frage zu der verwendeten Formel:

Warum wird 8% + 18% gerechnet?

---

Sehr gern :-)

Der Zeuge gibt in 8% + 18% = 26% aller Fälle an, dass das Taxi blau war (in 2% + 72% = 74% der Fälle gibt er an, dass das Taxi gelb war; so kommen wir auf insgesamt 100%).
Bei 100 "Versuchen" sagt er also 26mal: Das Taxi war blau. Von diesen 26 Aussagen sind aber nur 8 richtig; um seine "Trefferquote" für die Aussage "blau" zu bestimmen, müssen wir also 8 durch 26 dividieren, und das sind 8 / (8 + 18).

Man kann sagen: 8 + 18 = 26 ist die Gesamtanzahl aller Aussagen "blau",
und 8 ist die Anzahl der "günstigen", also richtigen Aussagen.

Man teilt dann günstig/gesamt.

Nachvollziehbar?

Besten Gruß

Answer 2

Brucybabe hat die Vierfeldertafel schon richtig aufgestellt. Die wäre zwar nicht ganz nötig gibt hier aber eine gute Übersicht. Eigentlich gibt es aber hier nur 2 Fälle die eintreten können.

Das Taxi war blau und der Zeuge sagt die Wahrheit. P = 0.08

Das Taxi war eigentlich Geld und der Zeuge irrt sich. P = 0.18

Wenn man jetzt fragt mit welcher Wahrscheinlichkeit ist das Taxi blau, müssten wir rechnen

P = 0.08 / (0.08 + 0.18) = 4/13 = 30.77%

Das Taxi war also zu etwa 31% blau und zu 69% gelb.

Comments

Oops, drei Antworten, drei Ergebnisse :-(

---

Ja, bei Mathecoach ist der letzte Schritt nur unlogisch. Seine Wahrscheinlichkeit gibt die Wahrscheinlichkeit an, dass der Zeuge sich nicht irrt unter der Bedingung, dass er die Wahrheit sagt. :)

MfG

Mister

---

PS: Eine Aussage, die für die Polizei allerdings unerheblich sein dürfte.

---

Man sollte nicht sagen das etwas unlogisch ist nur weil man es gerade nicht nachvollziehen kann. Für mich ist es logisch :)

Wie ich geschrieben habe gibt es von den Wahrscheinlichkeiten nur 2 Fälle.

Das Taxi war blau und der Zeuge sagt die Wahrheit. P = 0.08
Das Taxi war eigentlich Gelb und der Zeuge irrt sich. P = 0.18

Es kann ja nicht angehen das der Zeuge sich nicht irrt und das Taxi gelb ist.

Also sind die 0.08 und die 0.18 unsere Grundmenge von 100%

Und der Anteil wo das Taxi blau ist ist 0.08 / (0.08 + 0.18)

---

Wenn das Taxi eigentlich gelb war und der Zeuge sich irrt, so lautet seine Zeugenaussage "blau".

---

Ich bin mir übrigens nicht sicher ob das wirklich ein Beispiel für das Simpson-Paradoxon ist. Ich habe das Simpson-Paradoxon anders in Erinnerung. Das es dort um die Addition zweier Vieferldertafel ging. Das ist hier ja eigentlich nicht der Fall.

Aber ich meine dieser Fall der Taxis ist auch ein sehr bekanntes Paradoxon. Die meisten würden halt sagen das Taxi wäre zu 80% blau wenn der Zeuge sich in 80% aller Fälle nicht irrt.

---

Wenn das Taxi eigentlich gelb war und der Zeuge sich irrt, so lautet seine Zeugenaussage "blau".

Korrekt. Der Zeuge hat ja zu 100% schon mit "blau" geantwortet. Das können wir ja so hinnehmen.

Und dann gibt es halt 2 Möglichkeiten. Er irrt nicht und es war wirklich blau oder er irrt und es war eigentlich gelb.

---

Hm, sagen wir, mathecoach's Antwort ist richtig. Dann besteht das Paradoxon darin, dass trotz der hohen Trefferquote des Zeugen seine Aussage nur mit 31%iger Wahrscheinlichkeit richtig ist.

Meine Antwort ist insofern die richtige Antwort zur falschen Frage. ;)

Answer 3

ich würde vermuten, dass es "Simpson-Paradoxon" heißt, weil die Ereignisse eigentlich unabhängig sind: Ob der Zeuge richtig oder falsch (Y) liegt ist von der Wahrscheinlichkeit, ob es ein blaues oder gelbes Taxi war (X), unabhängig.

Die Wahrscheinlichkeit für "blau" beträgt P(X = blau) 20/200 = 10 %.

Die Wahrscheinlichkeit für "richtige Zeugenaussage" beträgt P(Y = richtig) = 80 %.

Die Wahrscheinlichkeit, dass "blau" und "richtig" gilt, ist P(X = blau)*P(Y = richtig) = 8 %.

Die Wahrscheinlichkeit, dass "gelb" und "falsch" gilt, ist P(X = gelb)*P(Y = falsch) = 18 %.

Die Summe dieser beiden Wahrscheinlichkeiten beträgt:

P("Polizei geht von blaumen Taxi aus") = 8 % + 18% = 26 %.

Das Paradoxon besteht offenbar in diesem geringen Prozentwert.

MfG

Mister

Comments

Oops, drei Antworten, drei Ergebnisse :-(