Integral rechnen senkrechte Pyramide mit Spitze im Punkt (0, 0, 1) und quadratischer Grundfl¨ache

Question

Berechnen Sie integral (V) z dx dy dz, wobei V eine senkrechte Pyramide mit Spitze im Punkt (0, 0, 1) und quadratischer Grundfläche mit Eckpunkten (±1, ±1, 0) ist.

das ist die frage und lösung ist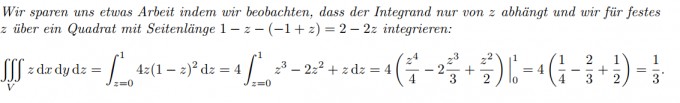 

aber von dieser lösung habe ich nichts verstanden kann mir bitte jemand bisschen besser erklären villeicht?

Answer 1

Aus den angegebenen Koordinaten geht hervor: Die Pyramide steht auf dem Nullpunkt und die Seiten haben einen Winkel von 45° (z.B. die Wand von "vorne" betrachtet hat die Mitte ihrer Unterkante bei (1/0/0) und deren Ecken bei (1/-1/0) und (1/1/0). Die Spitze ist bei (0/0/1). Die Grundfläche ist ein Quadrat mit Seitenlänge 2, auf halber Höhe der Pyramide hat das Quadrat noch die Seitenlänge 1 und an der Spitze die Seitenlänge 0.

Der Lösungsweg der Musterlösung integriert diese Quadratfläche mit abnehmender Seitenlänge, und zwar von Höhe 0 (Grundfläche) bis Höhe 1 (Pyramidenspitze) und erhält so das Volumen (Term nach dem ersten Gleichungszeichen).