ganzrationale Funktion 3. Grades Planungskosten, Verkaufserlös und Gewinn

Question

die Entwicklungsabteilung beginnt neun Monaten vor dem geplanten Verkaufsstart mit ihrer Arbeit (-9;0). Die Kosten und der Ertrag können durch folgende ganzrationale Funktion 3. Grades angenähert werden: f₃(x)=-5x³+195x²-19440.

a, Bestimme den Beginn der Gewinnzone und Ende des Verkaufszeitraums. (Nullstellenberechnung mit x₃=-9)

b. Ermittle den Monat, in dem der höchste Gewinn erwartet wird und berechne die Höhe des erwarten Gewinn (Nullstellenbestimmung der 1. Ableitung)

c.Gib die höchsten monatlichen Kosten an.(Weitere Nullstelle der 1.Ableitung)

d.Berechne die gesamten Planungskosten,den gesamten Verkaufserlös und den erwarteten Gesamtgewinn.Verwende dazu Rechtecke mit der Länge 13,5 für die Kosten der Länge 15,5 für den Erlös.(falls b und c nicht lösen kannst:H(26;24.500) T(0;-19.440))

Skizze zur Aufgabe

Answer 1

Zu a) Polynomdivision (-5x³+195x²-19440)/(x+9)=-5(x²-48x+432). Quadratische Gleichung lösen:
x²-48x+432=0. Lösungen x₂=12,x₃=36.

Comments

Die vom Aufgabensteller angegebene kubische Funktion (es soll sich augenscheinlich um die Gewinnfunktion handeln) gibt an, dass man mit dem Produkt einen Gewinn erzielt bevor man begonnen hat das Produkt zu entwickeln (sehr mysteriös), ab dem Zeitpunkt -9 dann anfängt Kosten zu generieren, ab dem Verkaufsstart zum Zeitpunkt 0 die monatlichen Verluste reduziert und bei der zweiten Nullstelle im Zeitpunkt 12 anfängt, Gewinn zu erzielen. Und zwar bis zur dritten Nullstelle im Zeitpunkt 36, ab welcher die Kosten monoton steigen, obwohl nichts mehr verkauft wird (auch mysteriös). Dabei wird übersehen, dass Monatsgewinne diskrete Werte sind.

a) Da kommt es darauf an, was mit "Gewinnzone" gemeint ist.

a1) monatliches Ergebnis anhand der kontinuierlichen Funktion: x=12

a2) monatliches Ergebnis anhand der diskreten Funktion: im 13. Monat erzielt man erstmals einen Gewinn, und zwar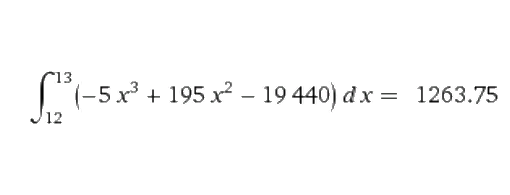

a3) falls damit das kumulierte Ergebnis gemeint ist (wahrscheinlich seit -9, denn von -∞ bis -9 ist laut Aufgabenstellung ja auch eine Gewinnzone), ist das Ergebnis nochmals anders.