Anwendungen von Funktionen

Question

Habe eine Aufgabe von meiner Lehrerin bekommen, um die Kostenfunktion, Erlösfunktion und Gewinnfunktion auszurechen benötige ich Menge und preis die ich ebenfalls berechnen muss.  Angegeben sind fixkostenanteil von 9 GE und variable Kosten von 0,02 GE und die Preis-Absatz Funktion p(x)=6-0.5x.

Wie berechne ich daraus jetzt den Preis pro Stück und die Menge ?

Danke für eure Hilfe im Voraus ☺️

Answer 1

Hallo DH,

a)  

Kostenfunktion:  K(x) =  0,02 * x + 9

Erlösfunktion:     E(x)  =  p(x) * x = (6 - 0,5 x) * x  =  6x - 0,5x²

Gewinnfunktion:

                      G(x)  =  E(x) - K(x) =  6x - 0,5x² - ( 0,02 * x + 9 )  =  - 25·x² + 299·x - 450

b)

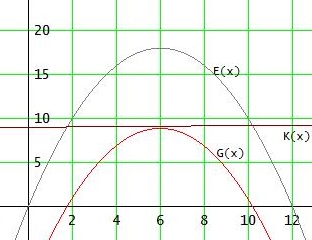
c)

 E(x)  =  6x - 0,5x²  

E '(x)  =  - x + 6 = 0   ⇔  x = 6

E(6)  =  18                Erlösmaximum (6 ME | 18 GE)

d) 

 G(x)  =  - 25·x² + 299·x - 450  = 0  ⇔  x² - 11,96·x + 18 = 0

pq-Formel   →   x₁ = 1.765691041  ;   x₂ = 10.19430895

Nutzenschwelle  ≈  1,7657  [ME]   ;    Nutzengrenze  ≈  10,1943 [ME]

e)

G'(x) = 2·x - 11.96 = 0    →   x = 5,98

x_max =  5,98  [ME]   ist die gewinnmaximale Ausbringungungsmenge

Gruß Wolfgang

Comments

Danke viel Mals ☺️

Aber wieso werden bei Aufgabe b Parabeln eingezeichnet und keine gerade Linien, den es geht ja um ein Koordinatensystem ?

---

Und wie genau komme ich bei Aufgabe D auf das Ergebnis von 11,96?

---

Indem du 299 durch 25 teilst.

---

Hallo Jessica,

> Aber wieso werden bei Aufgabe b Parabeln eingezeichnet 

Die Funktionsterme von E(x) und G(x) sind quadratische Polynome der Form ax² + bx + c .

Solche Graphen stellen immer Parabeln dar.

Gruß Wolfgang

---

Danke für die schnelle Antwort und Hilfe☺️

Eine Frage hätte ich noch, bei Aufgabe a bei der gewinnfunktion, könnte ich nicht auch G(x)=(6x - 0,5x²) - (0,02x + 9) = -0,5x² + 5,98x - 9 aufschreiben?  Laut meiner Berechnung würde das gleiche bei raus kommen. 11,96 x

---

Ja, denn die Terme 

(6 - 0,5 x) * x   und   6x - 0,5x²   sind gleichwertig.