Newton´sches Näherungsverfahren mit Extremwertaufgabe

Question

Ganzseitiges Foto.pdf (0,8 MB)

Ich habe bereits eine Zielfunktion ermitteln können:

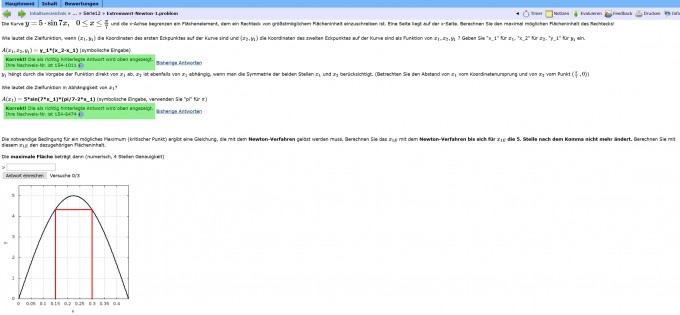
A(x1)= 5*sin(7*x_1)*(pi/7-2*x_1) 
 
"x_1" für x1


Diese soll nach dem Newton Verfahren gelöst werden. Das heißt Ableiten und 0 setzen, um das Extremum zu erhalten.
Leider weiß ich nicht, wie ich hier vorgehen muss. Mit dem Taschenrechner komme ich hier nicht wirklich weiter. Könnt ihr mir bitte etwas helfen, wie ich hier zur maximalen Fläche komme?

Als Newtonverfahren haben wir bisher folgende Formel genutzt:

x_Neu = x_Start - (f(x_Start) / (f (xStart)

Als Ableitung habe ich erhalten:
A(x) = 5 ((π - 14 x) cos(7 x) - 2 sin(7 x))

x= 0,1014947

Das x habe ich oben, bei der Flächenformel eingegeben und erhalten 0,0152397...., was leider zu klein ist :-(

Was habe ich falsch gemacht?

Answer 1

x = 0.101
Das x habe ich oben, bei der Flächenformel
eingegeben und erhalten
0,0152397...., was leider zu klein ist :-(

x = 0.101 in die Zielfunktion eingesetzt ergibt bei mir
A = 0.8

x = 0.101 erhalte auch ich als ersten
Maximalwert.

Comments

Oh man,  hatte lediglich mit Grad statt Bogenmaß gerechnet.  Und ich dachte,  ich befand mich irgendwo auf einem Holzpfad :-)

---

Schön, das der Fehler relativ rasch gefunden
werden konnte.

Answer 2

Als Ableitung habe ich erhalten:
A(x) = 5 ((π - 14 x) cos(7 x) - 2 sin(7 x))


Als Ableitung habe ich erhalten:
A(x) = 5 ((π - 14 x) cos(7 x) - 10 sin(7 x).