in diesem Semester war es in Mathe meine Aufgabe eine (von vielen) Methoden zu finden, mit der man die Kreiszahl PI annähern kann. Ich habe mich für die Exhaustionsmethode von Archimedes entschieden. Hier mal eine Skizze:
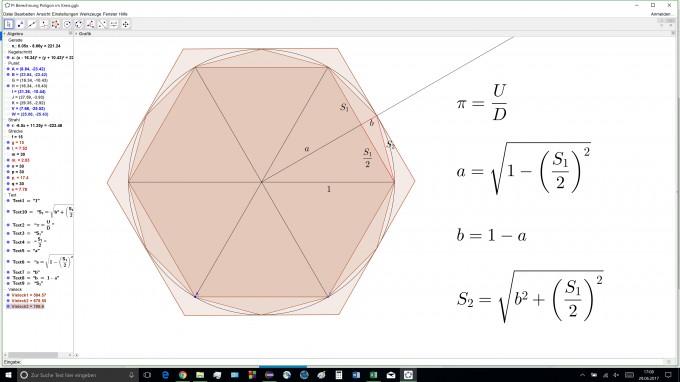
Wie man jetzt von innen heraus annähert ist mir bewusst, ich habe nur mit der äußeren approximation Schwierigkeiten.
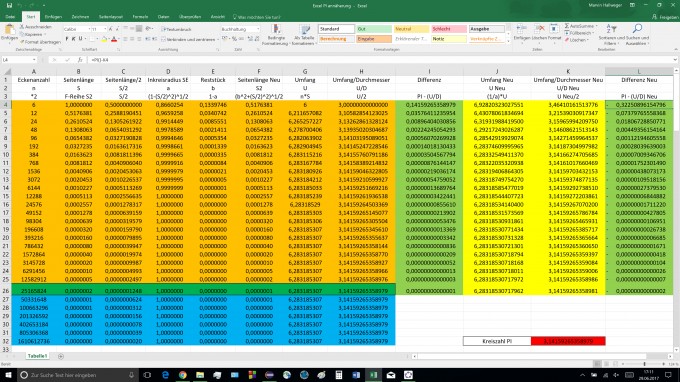
Die orangenen Spalten beschreiben die innere approximation, die hell grünen die Differenz PI- meine annäherung(en), die dunkelgrüne Zeile beschreibt den Fixpunkt und die blauen die darauffolgenden selben Ergebnisse. Die gelben Spalten sind meine äußere approximation.Meine Frage jetzt: warum muss man für die äußere approximation (1/a)*U rechnen? Wie kommt man da drauf? Ist das irgendeine Art von Strahlensatz? :) Wäre echt nett, wenn mir da jemand helfen würde :)
Und wenn ich jetzt schonmal frage: Bei diesen Differenzen (ich dachte das könnte das ganze vielleicht ein wenig verdeutlichen), sieht man am ende ein Intervall von [-0,0000000(...)002 ; 0,0000000(...)00001]. Deute ich das jetzt richtig, dass das der Bereich ist wo sich der Kreis befindet? Also auf dem Bild die Ecke bei b z.B? Da nähert sich ja alles an und ich dachte mir vielleicht, dass sich da vielleicht die Zahl PI befindet(?) Oder sind das diese 2 Schranken die Archimedes auch definiert hat? Bin jetzt gerade selber verwirrt :D