Aufgabe:
Bei der Familie Mustermann gibt es die Tradition, dass die Kinder Mausi und Klausi sich eine
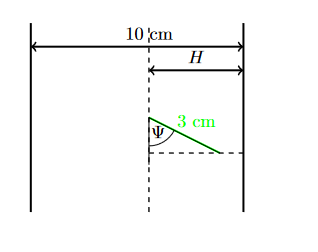
Approximation für π überlegen müssen, bevor der Weihnachtsmann die Geschenke verteilt. Dieses Jahr haben Sie sich das folgende Verfahren überlegt: Mausi schüttelt am Weihnachtsbaum damit möglichst viele Nadeln herunterfallen. Der Weihnachtsbaum steht in einem Zimmer mit Holzdielen, die eine Breite von 10cm haben. Alle der N Nadeln die herunterfallen, haben eine Länge von 3cm und eine zu vernachlässigende Breite. Zudem gehen wir davon aus, dass die Nadeln sich gleichmäßig und unabhängig voneinander auf dem Fußboden verteilen. Klausi bestimmt nun die Anzahl X der Nadeln, die mehr als eine Diele berühren und behauptet, dass 3N/5X eine gute Approximation für π sei. Stimmt das für große N ? Hinweis: Bestimme die Wahrscheinlichkeit für das Ereignis, dass eine Nadel mehr als eine Diele berührt. Die zufälligen Größen Ψ und H in der Skizze unten könnten Dir dabei helfen
Problem/Ansatz
Also ich muß zugeben, daß ich in meinen mittlerweile 15 Hochschulsemestern selten so sehr wie der sprichwörtliche Ochs vor'm Berg stand wie bei dieser Aufgabe. Pi ist doch 3,14... Wie soll jetzt 3N geteilt durch 5X, wobei N und X ja noch völlig unbekannte und willkürliche Werte sind, eine Annäherung durch Pi sein. Zumal in der Skizee nicht mal Ansatzweise ein Kreis zu erkennen ist. Wie soll frau jetzt mit diesen Infos die Wahrscheinlich, daß eine Nadel mehr als eine Diele berührt bestimmen? Wahrscheinlichkeit = Anzahl günstiger Ereignisse / Anzahl allgemeiner Ereignisse. Die günstigen Ereignisse wären, daß eine Nadel mehr als eine Diele berührt. Bei N Nadeln a l a 3 cm auf eine Diele mit 10 cm Breite, ist die Wahrscheinlichkeit auf eine Diele zu treffen 3 cm / 10 cm... Für N Nadeln dann 3/10 ???
Ich gehe zudem davon aus, dass wenn die Aufgabenstellung schon so fragt, die Annäherung für große N bestimmt nicht zutreffen wird.
Liebe Grüße,