Bestimmen Sie die Fläche des aufgespannten Parallelogramms

Question

Aufgabe:

Bestimmen Sie die Fläche des von den Vektoren \( \left(\begin{array}{l}2 \\ 3\end{array}\right),\left(\begin{array}{l}3 \\ 4\end{array}\right) \) aufgespannten Parallelogramms.

Problem/Ansatz:

Wie genau mach ich den das. Mir ist bewusst, wie ich das mache wenn die Vektoren 3 Zahlen haben und dann übers Kreuzprodukt usw. , aber wie mache ich das mit nur 2 Zahlen.

Comments

Betrag des Kreuzprodukts = Flächeninhalt des Parallelogramms

---

Das Kreuzprodukt ist für den R^2 gar nicht definiert. DAS war das Problem der gestellten Frage!

---

Dong, danke. Nicht alles was lang ist, ist eine Leitung.

Answer 1

Da die beiden Vektoren in die xy-Ebene passen (wo die z-Koordinate 0 ist), kannst du sie -wenn du unbedingt das Vektorprodukt verwenden willst- zu  \( \left(\begin{array}{l}2 \\ 3\\0\end{array}\right),\left(\begin{array}{l}3 \\ 4\\0\end{array}\right) \) ergänzen.

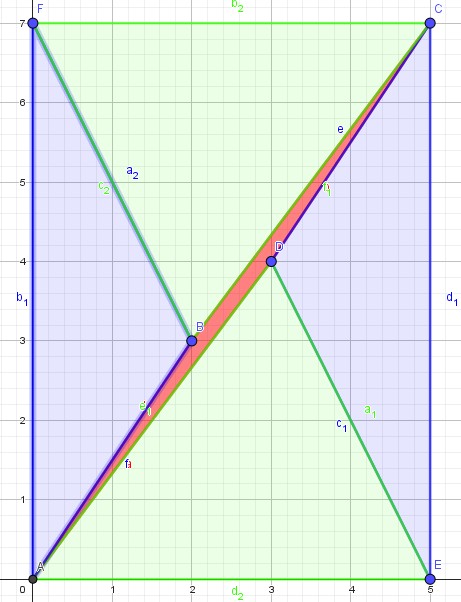
Ganz ohne Vektorprodukt kann ein einigermaßen pfiffiger Schüler mit Mitteln der Klasse 7 den Inhalt deines (hier rot dargestellten) Parallelogramm als "Rechteck minus 4 Dreiecke" bestimmen.

Answer 2

Aloha :)

Du kannst z.B. die Komponenten einfach "über Kreuz" rechnen:$$F=|2\cdot4-3\cdot3|=1$$Oder du verwendest das Vektorprodukt. Da dieses jedoch nur im \(\mathbb R^3\) defniert ist, setzt du die \(z\)-Koordinate gleich \(0\):$$F=\left\|\begin{pmatrix}2\\3\\0\end{pmatrix}\times\begin{pmatrix}3\\4\\0\end{pmatrix}\right\|=\left\|\begin{pmatrix}0\\0\\-1\end{pmatrix}\right\|=1$$

Comments

\(F=\left\|\begin{pmatrix}2\\3\\0\end{pmatrix}\times\begin{pmatrix}3\\4\\0\end{pmatrix}\right\|=\left\|\begin{pmatrix}0\\0\\2\end{pmatrix}\right\|=2\)

Über die letze 2 im Vektorprodukt würde ich nachdenken.

---

Oops, \(3\cdot3\) ist ja gleich \(9\)... hab's korrigiert.

Danke für den Hinweis.