die Formel für den Flächeninhalt des Rechtecks ist
A = 2u * (g(x) - f(x))
g(x) - f(x) sind in der Zeichnung die Seiten b und d
Die Gleichungen einsetzen ergibt
A = 2u*(0,5u^2- 2 - (-0,25u^2+4))
Ich spare mir jetzt die Rechenwege, die zu
A = -12u + 1,5u^3
führen. Falls du sie brauchst, bitte Info.
Um die Extremstellen zu finden, setzt du die erste Ableitung null,
also
A' = 4,5u^2 - 12
4,5u^2 - 12 = 0
Das Ergeb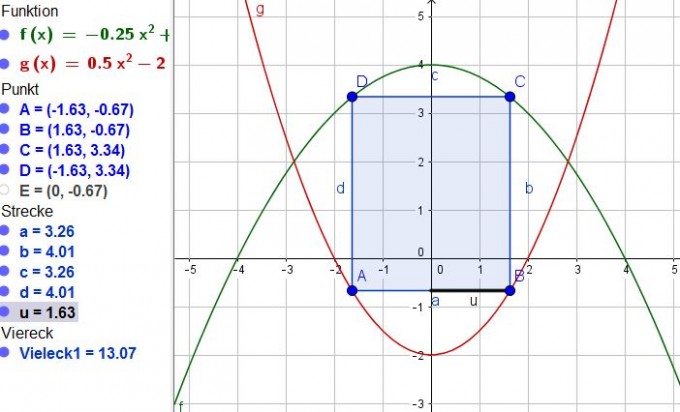 nis ist
nis ist
u = ± 1,63
Jetzt musst du für x in die beiden Gleichungen 1,63 und -1,63 einsetzen, um die y-Koordnaten der Punkte zu erhalten.
Gruß
Silvia