Extremwertproblem mit Wurzelfunktion

Question

Aufgabe:

Extremwertproblem:

Bei dieser Aufgabe ist die Funktion h(x)= \( \sqrt{x} \) über dem Intervall [0;9] gegeben. Hierbei soll der Kurvenpunkt P(u^2/u) mit 0<u<3 bestimmt werden, durch den eine Gerade g parallel zur X Achse gelegt werden muss, damit die schraffierte Fläche in ihrer Größe A(u) minimal wird. Die schraffierte Flasche geht dabei vis zum Punkt P, und von P bis 9 und liegt dabei zwischen U und der funktioniert. h(x)

Comments

es ist unklar, wie die 'schraffierte Fläche' aussieht. Meinst Du alles was zwischen der X-Achse und \(h(x)\) liegt, was nicht(!) von dem lila Rechteck abgedeckt wird? Mit \(x\le9\).

---

Das stimmt. Also ich meine mit der schraffierten Fläche das Stück über dem lila Kasten (also zwischen rotem Graph und der gestrichelten schwarzen Line), sowie 0;5 unter der gestrichelten Linie und über der roten Kurve

---

Also Du meinst die blau markirte Fläche hier im Bild:

Ist das richtig? Die Lösung wäre dann \(u_{\min} =\frac32 \sqrt2\) ... muss man jetzt bloß noch ausrechnen ... ;-)

---

Genau, die blaue Fläche. Was wäre denn hier der Ansatz. Ich verstehe genau gerade nicht, wie man das ausrechnet und, wie du auf 3/2 Wurzel (2) gekommen bist ?

Answer 1

Hallo,

Ich verstehe genau gerade nicht, wie man das ausrechnet

Man zählt halt alles zusammen, bzw. schneidet Flächen entsprechend ab. Mit etwas Übung lässt sich für die gesuchte Fläche \(F\) schreiben:$$F=u^{3}-\int_{0}^{u^{2}}h\left(t\right)dt+\int_{u^{2}}^{9}h\left(t\right)dt\ -u\left(9-u^{2}\right)$$Das \(u^3\) ist das Rechteck mit der Diagonalen \((0|\,0)\) und \(P\). Das erste Integral ist die Fläche unter \(h(x)\) im ersten Intervall. Die Differenz ist die linke blaue Fläche. Und dann zeiht man von dem Integral des rechten Intervalls das Rechteck mit der Diagonalen \(P\) bis \((9|\,0)\) wieder ab.

Das rechne ich aber gar nicht aus, sondern ich nutze die Information, dass eine halbe Parabel die von einem achsenparallelen Rechteck derart umhüllt wird, dass eine Ecke des Rechtecks im Scheitelpunkt liegt, genau \(2/3\) der Fläche des Rechtecks einnimmt.

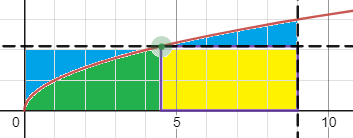
Das Rechteck links (blau/grün) hat die Fläche \(u^3\). Die grüne Fläche \(F_2\) ist demnach \(F_2=\frac23u^3\). Die linke blaue Fläche \(F_1\) ist der Rest \(F_1=\frac13 u^3\). Die Fläche unter der Kurve von \(u^2\) bis \(9\) ist die gesamte Parabel \(= \frac23 \cdot 27 = 18\) minus \(F_2\). Und davon ziehe ich noch das gelbe Rechteck darunter ab (\(u(9-u^2)\)). Alles zusammen macht$$F = \underbrace{\frac13u^3}_{\text{blaue(links})} + \underbrace{18-\frac23u^3}_{\text{blau(rechts) + gelb}} - \underbrace{u(9-u^2)}_{\text{gelb}}\\\phantom F= \frac23u^3 - 9u+18$$ Ableiten und zu 0 setzen gibt \(u^2=\frac92\) bzw. \(u=\frac32\sqrt 2\); die negative Lösung liegt außerhalb des Definitionsbereichs und entfällt daher.

... und, wie du auf 3/2 Wurzel (2) gekommen bist ?

um ehrlich zu sein, ich habe es ausgemessen ;-) da ergab sich \(u^2=9/2\)

Gruß Werner

Comments

Warum muss man am Ende eigentlich ableiten und = 0 setzten ?

---

Warum muss man am Ende eigentlich ableiten und = 0 setzten ?

Das Ziel ist es doch, das Minimum der Fläche zu berechnen. Ein Minimum ist ein Extremum einer Funktion, was sich u.a. dadurch auszeichnet, dass die Ableitung dort gleich 0 wird. Also muss man zunächst ableiten ... $$F(u)=\frac23u^3-9u+18\\F'(u)=2u^2-9$$und dort, wo \(F(u)=0\) wird, darf man ein Extremum vermuten$$F(u_{e}) = 0=2u_e^2-9 \implies u_e=\frac32\sqrt 2$$Um das Abzusichern berechnet man die 2.Ableitung an dieser Stelle$$F''(u)= 4u \implies F''\left(u=\frac32\sqrt 2\right) \gt 0$$D.h. es liegt tatsächlich ein Minimum vor.

Ich habe das auch in den Graphen eingetragen:

der X-Wert(!) des blauen Graphen gibt den Wert der besagten Fläche an. Ich habe das so aufgetragen, weil \(u\) auf der senkrechten Kordinatenachse abgetragen wird. man sieht, dass ein Minimum erreicht wird, wenn der X-Wert von \(P\) genau auf der Hälfte des Intervalls liegt.

---

Besser hätte man es nicht erklären können. Vielen Dank !

Answer 2

Bei dieser Aufgabe ist die Funktion h(x)= \( \sqrt{x} \) über dem Intervall [0;9] gegeben. Hierbei soll der Kurvenpunkt P(u^2/u) mit 0<u<3 bestimmt werden, durch den eine Gerade g parallel zur X Achse gelegt werden muss, damit die schraffierte Fläche in ihrer Größe A(u) minimal wird. Die schraffierte Fläche geht dabei bis zum Punkt P, und von P bis 9 und liegt dabei zwischen U und der Funktion h(x)

Ich nehme mal den Vorschlag von Werner-Salomon:

Schraffiertes Rechteck A(u)=(9-u^2)*u=9u-u^3 soll maximal werden.

A´(u)=9-3u^2=0        u^2=3   P (3 |\( \sqrt{3} \))

Comments

Habe oben beschrieben, wie die schraffierte Fläche aussehen muss. Vielleicht hilft es weiter. Aber wie bist du auf den Ansatz gekommen