Aufgabe:
Das Ziel ist es Q so zu wählen, dass die Fläche, die von der Y-Achse bis Q und g(x)
Bis x=2 eingeschlossen wird, maximal ist.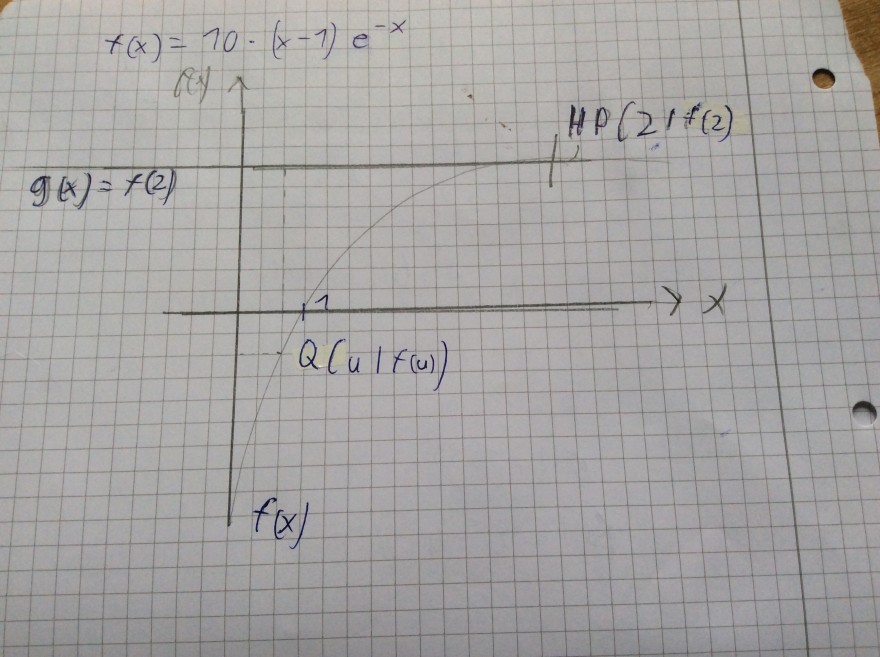
Problem/Ansatz:
Man stellt die Funktion A(u)=u*( |f(u)| + g(x) ) , die man dann bis x=1 benutzen kann, auf
Mit dieser Funktion hat man den Betrag von der Länge, die man durch f(u) bekommt
Und noch das zusätzliche Stück also g(x)
Und dann macht man noch die Funktion für nach x=1 aber dort ist die Fläche kleiner als
Die bis x=1 deshalb schreibe ich die nicht mehr auf.
Dann macht such man den Hochpunkt von A(u) und so weiter.
Ist die aufgestellte Funktion so richtig?)