Extremwertproblem mit Nebenbedingung

Question

Aufgabe:

Und zwar ist eine Figur gegeben, die aus einem Rechteck und zwei gleichseitigen Dreiecken zusammengesetzt ist. Jetzt ist gefragt, wie lang das Rechteck sein muss, wenn der Flächeninhalt maximal sein soll und der Umfang 100 cm betragen soll

Problem/Ansatz:

Komme hier gar nicht weiter. Hatte jetzt anfangs gedacht dass ich die beiden Dreiecke nicht beachten muss, da in der Aufgabe nur nach dem Rechteck gefragt ist. Komme gar nicht weiter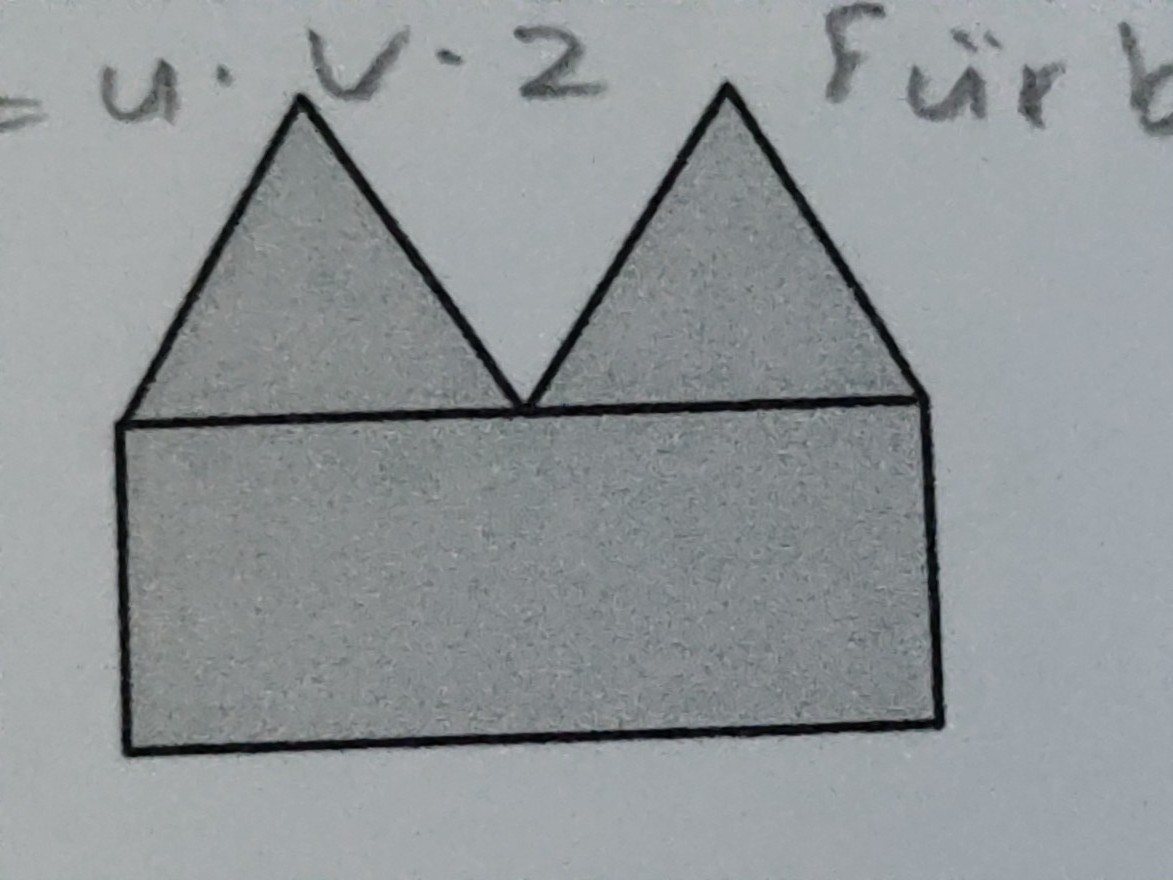

Text erkannt:

\( B \)

Comments

da in der Aufgabe nur nach dem Rechteck gefragt ist

Bist Du da sicher? Die Rede ist doch von Flächeninhalt und Umfang einer Figur, "die aus einem Rechteck und zwei gleichseitigen Dreiecken zusammengesetzt ist".

Answer 1

100=6a+2b dann ist (1) b=50-3a

Flächeninhalt: A=a·b+2·a²/4·√3 oder (2) A=a·b+a²/2·√3.

(1) in (2): A(a)=a(50-3a)+a²/2·√3.

Nulllstelle der ersten Ableitung ist das a für den maximalen Flächeninhalt F(a).

Answer 2

a+2b+4*a/2 = 100

3a+2b= 100

b = 50- 1,5a

A= a*b+ 2*(a/2)^2/4* √3

A(a) = a*(50-1,5a)+ a^2/4*√3 = 50a-1,5a^2+a^2/4*√3 = 50a- a^2*(1,5-√3/4)

A'(a) = 0

a= ...