Wahrscheinlichkeiten von Krankheiten

Question

1% der Bevölkerung leidet unter einer bestimmten Krankheit. Es gibt zwar einen medizinischen Test, um die Krankheit festzustellen, allerdings ist dieser nicht perfekt. Nur bei 95% der Erkrankten wird die Krankheit tatsächlich angezeigt. Umgekehrt kommt der Test bei 4% aller Gesunden zum Ergebnis, dass sie krank seien.

• Angenommen bei einer zufällig ausgewälten Person wird der Test durchgeführt. Mit welcher Wahrscheinlichkeit zeigt der Test an, dass die Person erkrankt ist?

• Bei Herrn Meier zeigt der Test an, dass er krank sei. Mit welcher Wahrscheinlichkeit ist er wirklich krank?

Answer 1

Hallo JF,

nur vorsichsthalber: "Test positiv"  ist die schlechte Nachricht:

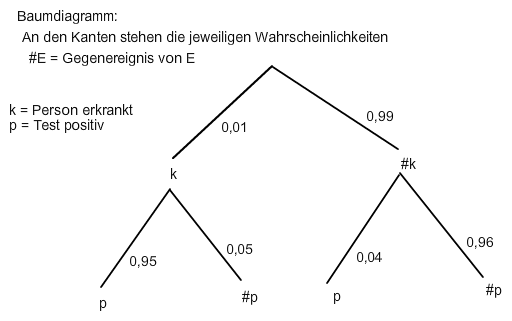
1)  Gesucht ist  P("Test ist positiv")

P(p)  =  0.01 * 0.95 + 0.99 * 0.04 = 0.0491 =  4,91 % 

2)  Gesucht ist P("Person ist krank unter der Bedingung, dass der Test positiv ist") 

 P(k|p)  = P(k∩p) / P(p) =  0.01 * 0.95 /  0.0491  ≈  0.193 = 19,3 %

------

Ein positiver Test ist also erst einmal kein Grund zum Verzweifeln sondern für weitere Untersuchungen.

Du kannst ja mal nachrechnen, dass umgekehrt

 P("Person ist gesund unter der Bedingung, dass der Test negativ ist") = 99 % gilt.

Gruß Wolfgang