Question

Bestimmen Sie die letzte Ziffer von 2¹⁰⁰.

Lösungshinweis: Ziehen Sie die mod-Rechnung heran. Der Ansatz 2¹⁰⁰ = (2⁵)²⁰ führt auf eine Lösungsspur.

Answer 1

Lösungsweg 1:

pow(2,100) diese kleine Zahl kann doch jeder gute Rechner wie 

http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php

1267650600228229401496703205376

Weg 2:

2^n mod 10 ergibt die periodische Folge 2,4,8,6,2,4,8,6,...

also ist 2^{4n} mod 10 = 6

analog auch (2^5)^{4n} mod 10 =6

Weg 3:

Pow-Mod-Algorithmus wie unter 

http://www.lamprechts.de/gerd/Roemisch_JAVA.htm#ZZZZZ0122

beschrieben

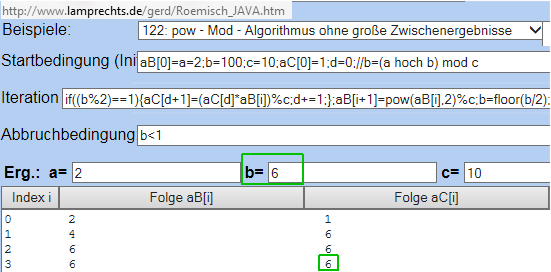
x^y = pow(x,y) und x mod y = x % y

Und wenn Du mal richtig große PowPowMod berechnen willst

schau Dir das mal unter http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php

an... :-)

Answer 2

2^100 mod 10

(2^5)^20 mod 10

(32)^20 mod 10

(32 mod 10)^20 mod 10

(2)^20 mod 10

(2^5)^4 mod 10

(2)^4 mod 10

16 mod 10

6