Berechnen Sie den Schnittpunkt der Seite b mit der Geraden g: y=x

Question

Ich wollte wissen, ob meine beiden Lösungen stimmen, da ich keine Lösungen zum Lernen bekommen habe.

a) y= -3/2x + 11/2 Rechenweg: Ich habe einfach die beiden Punkte B und C genommen und die Steigung dazu berechnet.

und b) wäre (0/5/2) Hier habe ich die Steigung mit A und C berechnet, aber da es sich bei q schneidet, den als Schnittpunkt angegeben.

Answer 1

Hallo Sliverdart,

Tipp: mache Dir immer eine Zeichnung.

(a) Die Schwerlinie \(s_a\) ist die Gerade, die durch \(A\) und die Mitte \(S_a\) der Seite \(a\) verläuft. \(S_a=0,5\cdot (B+C)=0,5\cdot ((5|1)+(1|7))=(3|4)\). Die Steigung \(m\) berechnet sich aus der Differenz von \(S_a\) zu \(A\):

$$m=\frac{4 - (-2)}{3 - (-1)}= \frac{6}{4}=1,5$$

Die Gerade geht durch \(S_a=(3|4)\), demnach lautet die Geradengleichung

$$y(x) = 1,5 \cdot (x - 3) + 4 = 1,5 x - 0,5$$

Die Zeichnung zeigt, dass das Ergebnis korrekt ist (blaue Gerade):

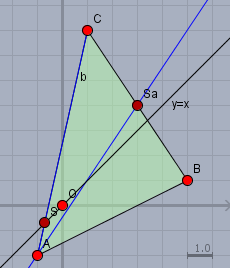
(b) Die Seite \(b\) hat die Steigung \(9/2=4,5\) und verläuft durch \(C=(1|7)\):

$$y(x) = 4,5 \cdot (x- 1) + 7=4,5 x + 2,5$$

Einsetzen von \(y=x\) ergibt:

$$x_s=4,5 x_s + 2,5 \quad \Rightarrow x_s = -\frac{5}{7}$$

Der Schnittpunkt \(S\) liegt also bei \(S=(-\frac{5}{7}|-\frac{5}{7})\).

Gruß Werner

Answer 2

a)

Mittelpunkt der Strecke BC

M = 1/2·([5, 1] + [1, 7]) = [3, 4]

Seitenhalbierende durch A und M

y = (4 - (-2)) / (3 - (-1))·(x + 1) - 2 = 3/2·x - 1/2 = 1.5·x - 0.5

b)

Gerade b durch A und C

y = (7 - (-2)) / (1 - (-1))·(x + 1) - 2 = 9/2·x + 5/2 = 4.5·x + 2.5

Schnittpunkt der Seite b  mit g

4.5·x + 2.5 = x --> x = -5/7 = -0.7142857142

y = -5/7 --> S(-5/7 | -5/7)