Textgleichung: Rechteck mit Parallele zur kleinen Seite; neues Rechteck, wie lang ist kleine Seite des neuen?

Question

Egal, wie ich die folgende Aufgabe im wahrsten Sinne des Wortes drehe und wende, komme ich nicht auf die vorgegebene Lösung oder überhaupt irgendeine:

In einem Rechteck mit den Seiten a = 6 cm soll durch eine Parallele zur kleinen Seite ein kleines Rechteck abgeschnitten werden, das dem ursprünglichen ähnlich ist. Wie lang ist die kleinere Seite des neuen Rechtecks?

Lösung soll 4,5 cm sein.

Folgende Überlegungen:

x = gesuchte kleine Rechteckseite

y = große Seite des neuen Rechtecks und kleine Seite des Ursprungsrechtecks

6 cm = große Seite des Ursprungsrechtecks

 

6 cm > y > x > 0 cm

 

Weiter komme ich nicht und mehr ist nicht gegeben.

Answer 1

Da die Aufgabe ansonsten nicht zu lösen ist, gehe ich davon aus, dass in der ursprünglichen Aufgabenstellung a und b gegegen sind. Darauf weist auch "[...] In einem Rechteck mit den Seiten a = 6 cm [...]" hin. Mit der gegebenen Lösung für c, lässt sich b bestimmen -- b = 8 cm.

Die Lösung sieht dann mit der Annahme a = 6cm und b = 8cm wie folgt aus:

 

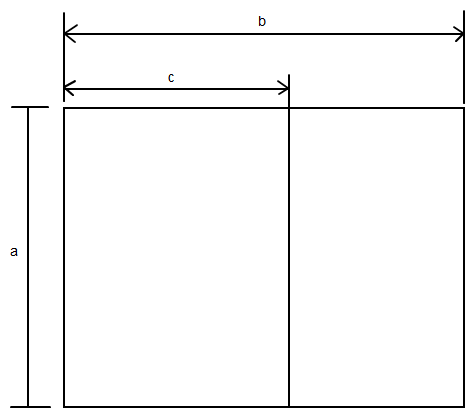
Mit a = 6cm, b = 8 cm.

 

Da die Rechtecke ähnlich sind gilt für das Verhältnis der Seiten von kleinem und großem Rechteck:

$$ \frac{a}{b} = \frac{c}{a} $$

 

Umstellen nach c, der gesuchten Seite, liefert...

$$ c = \frac{ {a}^{2} }{b} = \frac{ {(6 cm)}^{2} }{8 cm} = \frac{ 36 {cm}^{2} }{8 cm} = 4,5 cm $$

 

Die kurze Seite ist 4,5 cm lang.