Bestimmen Sie die Länge der Kurve γ2 := { (−t^2 , 2t^3 ), t ∈ [0, 1] }

Question

Jo ich muss wie schon im Titel erwähnt die Länge der Kurve bestimmen:

γ2 := { (−t^2 , 2t^3 ), t ∈ [0, 1]  }

So habe ichs gemacht (glaube aber nicht dass das richtig ist):

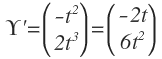
$$||\Upsilon '||=\sqrt { { (-2t) }^{ 2 }+(6t^{ 2 })^{ 2 } } =t\sqrt { 4+36t^{ 2 } } =t(2+6t)$$

$$L=\int _{ 0 }^{ 1 }{ t(2+6t)dt } =t^{ 2 }+2t^{ 3 }{ | }_{  0}^{1 }=1+2-0=3$$

ich glaube nicht, dass diese Lösung stimmt...

Answer 1

Hi,

es ist $$ t\sqrt { 4+36t^2 }\neq t(2+6t) $$

Forme stattdessen zu

$$ t\sqrt { 4+36t^2 }= 2t\sqrt { 1+9t^2 } $$

um und setzte dies im Integral ein.

Das Integral kannst du dann durch die Substitution u=1+9t^2 lösen.

Comments

stimmt... xD wie hab ich denn das hinbekommen, aber ich lerne auch schon seit 6-7 stunden wahrscheinlich war das der grund für den dummen fehler...

---

also wie soll ich das nochmal genau integrieren?

mit u= 1+9t^2  klappt das nicht so richtig?

---

hab soweit sowas:

ist das soweit richtig? wie gehts jetzt weiter? resubstitution dann grenzen einsetzen?

---

Oh vergessen die Grenzen mit zu substituieren...

also obere ist √10 und untere 1...

soll ich jetzt einfach resubstituieren und die grenzen einsetzen, wenn alles soweit richtig?

Answer 2

Meine Rechnung:

  :

Comments

Teil2 :