Verständnisfrage zu komplexen Zahlen. Für welche z∈ℂ gilt? z.B. |z+j|=1

Question

ich habe hier ein paar Übungsaufgaben zu komplexen Zahlen und weiß einfach nicht, wie ich dabei vorgehen soll und in meinen Fachbüchern finde ich irgendwie auch nichts dazu.

Folgende Aufgabe: Für welche z∈ℂ gilt?

z.B. |z+j|=1

oder

Im(z)≤Re(z)^2 -1

Ich möchte einfach nur wissen, wie man bei solch Aufgaben vorgehen sollte.

Comments

Die Lösung von Im(z)≤Re(z)² -1  habe ich bereits herausgefunden, dass sind alle komplexen Zahlen auf/unterhalb von y=1/4 x^2 liegen.

---

Ok. Interessant!

Hast du Im(z)≤Re(z)² -1  interpretiert als Im(z)≤Re((z)² ) -1  ? 

y ≤ Re( (x+iy)^2) - 1 = Re ( x^2 + 2ixy - y^2) - 1 = x^2 - y^2 - 1 ? 

y^2 + y  ≤ x^2 -1 

y^2 + y + 1/4 ≤ x^2 - 1 + 1/4 

(y + 1/2)^2 ≤ x^2 - 3/4 

3/4 ≤ x^2 - (y + 1/2)^2 

Mit der unwahrscheinlichen Lesart: 

Im(z)≤(Re(z))² -1   ? 

Damit komme ich zu

y ≤ x^2 - 1 

---

Upsi, da hatte ich das falsche Ergebnis abgeschrieben. Mein Fehler. Richtig ist natürlich:

Im(z)≤(Re(z))² -1
Im(x+jy)≤(Re(x+jy))^2 -1
y≤x^2 -1

Answer 1

 |z+j|=1 

Betrag bedeutet bei komplexen Zahlen Länge des Pfeils in der komplexen Zahlenebene oder Abstand 2er Punkte in der komplexen Zahlenebene. Mit der zweiten Interpretation und der Schreibweise

 |z - (-j)|=1 

kommst du als Lösungsmenge auf die Menge aller Elemente der komplexen Zahlenebene, die von -j den Abstand 1 haben. Das gibt eine Kreislinie  k(M= -j , r = 1) . M: Mittelpunkt, r: Radius. 

In der folgenden Abbildung noch die Beschriftung der vertikalen Achse korrigieren. Das soll ja die imaginäre Achse sein. Also -2j, -1j, 1j, 2j, 3j, ... hinschreiben und statt x und y neben den Pfeilen reelle und imaginäre Achse schreiben. 

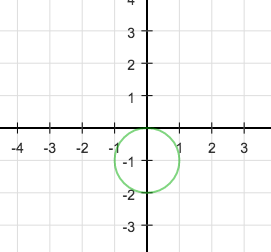
~draw~ ;kreis(0|-1 1)#;zoom(2) ~draw~

Comments

Im(z)≤Re(z)² -1  

Hier rechts bitte erst mal die Klammerung überprüfen und erklären.

Ist eher Im(z)≤ (Re(z)) ² -1

oder Im(z)≤Re((z)²) -1

oder Im(z)≤Re((z)² -1) 

gemeint? 

Weitere ähnliche Fragen findest du in der Rubrik "ähnliche Fragen" unten. Dort kannst du schon mal ein paar Ideen holen. 

---

Aber wenn ich versuche, das bei einer ähnlichen Aufgabe anzuwenden, kommt das dabei raus.

|z-j|=Im(z+j)

|x+jy-j|=Im(x+jy+j)

|x+j(y-1)|=Im(x+j(y+1))

|x+j(y-1)|=y+1 hier weiß ich nicht weiter

oder ich lasse

|z-j|=y+1 und komme nicht weiter

Ich meine der Mittelpukt wäre ja j oder nicht? Aber wie bekomme ich dann den Radius raus?

---

|x+j(y-1)|=y+1   | quadrieren und Pythagoras nutzen.

x^2 + (y-1)^2 = (y+1)^2 

x^2 + y^2 - 2y + 1 = y^2 + 2y + 1 

x^2 = 4y 

1/4 x^2 = y 

Also eine Parabel .

Erinnere dich daran, dass eine Parabel auch die Menge aller Punkte ist, die von einem Punkt (Brennpunkt) und einer Geraden denselben Abstand haben. 

https://de.wikipedia.org/wiki/Parabel_(Mathematik)#Definition_mit_Leitlinie 

---

oooooh, da hatte ich wohl wieder ein Brett vorm Kopf. Danke, jetzt weiß ich auch, wie ich die anderen Aufgaben lösen kann :).

Answer 2

setze

$$ z=x+iy $$

wobei x und y reelle Zahlen sind.

Löse dann auf und erhalte eine Beziehung zwischen x und y.

Damit kannst du die Lösungsmenge darstellen.

Answer 3

Setze z=a+jb

1. Aufgabe:

|a+jb +j|=1

|a+j(b+1)|=1

usw.

Comments

Danke erstmal für die Antwort, aber irgendwie werde ich immer noch nicht ganz schlau daraus. Wäre es vielleicht doch möglich, dass du mir die erste Aufgabe vorrechnest? Damit ich das hoffentlich dann nachvollziehen kann und die anderen Aufgaben selbst hinbekomme. 

---

hat sich dann wohl erledigt

---

Ja, trotzdem vielen Dank.

Answer 4

Weißt du wie du z ∈ C von

|z| = 1 darstellen kannst ?

Ist das ein Kreis mit Radius 1 um den Ursprung ?

Was passiert wenn du jetzt von z einfach die imaginäre Einheit abziehst ? Verschiebt sich dann nicht nur einfach der Kreis ?

|z + j| = 1