Warum ist das Integral für 0 bis 2pi von cos(2x)dx NULL?

Question

für Integration bei Fourierreihe möchte ich gern wissen: Warum ist für 0 bis 2π

a0/2 * Integral von (cos2x) dx

NULL? Gibt es für diese Form von Integral eine generelle Regel, sodass man nicht immer herleiten muss? Wie sieht es zum Beispiel mit cos(3x), cos (4x), sin (2x), sin (3x) aus?

Comments

Überleg dir die Ableitung des Integranden. Damit kommst du schnell auf die Stammfkt.

Answer 1

Hi,

Du darfst wissen, dass die Periode vom cos(2x) die Länge π hat. Wenn Du über die Periode oder ein Vielfaches davon integrierst, dann heben sich doch die Flächen unterhalb und überhalb der x-Achse weg (Symmetrie) und folglich ist der Wert des Integrals 0. So auch hier ;).

Alles klar?

~plot~ cos(2x); [[-0,25|7|-1,5|1,5]] ~plot~

(2π ≈ 6,28)

Grüße

Answer 2

Also, du hast ja mehrere Integral Flächen, ich habe die mal farblich gekennzeichnet mit Grün und Rot. Angenommen die Eine Fläche ist Positiv die andere gleichgroße Fläche ist negativ. Wenn ich diese beiden Flächen addiere bekomme ich 0 raus. Die Flächen heben sich also aufgrund der Symmetrieeigenschaften und der Periode auf! Wichtig die Fläche ist nicht negativ, das habe ich einfach nur zur Verdeutlichung als Beispiel genommen.

PS: Zu gerne würde ich dich persönlich bei deiner Prüfungsvorbereitung unterstützen. Ich mag diese Aufgaben!

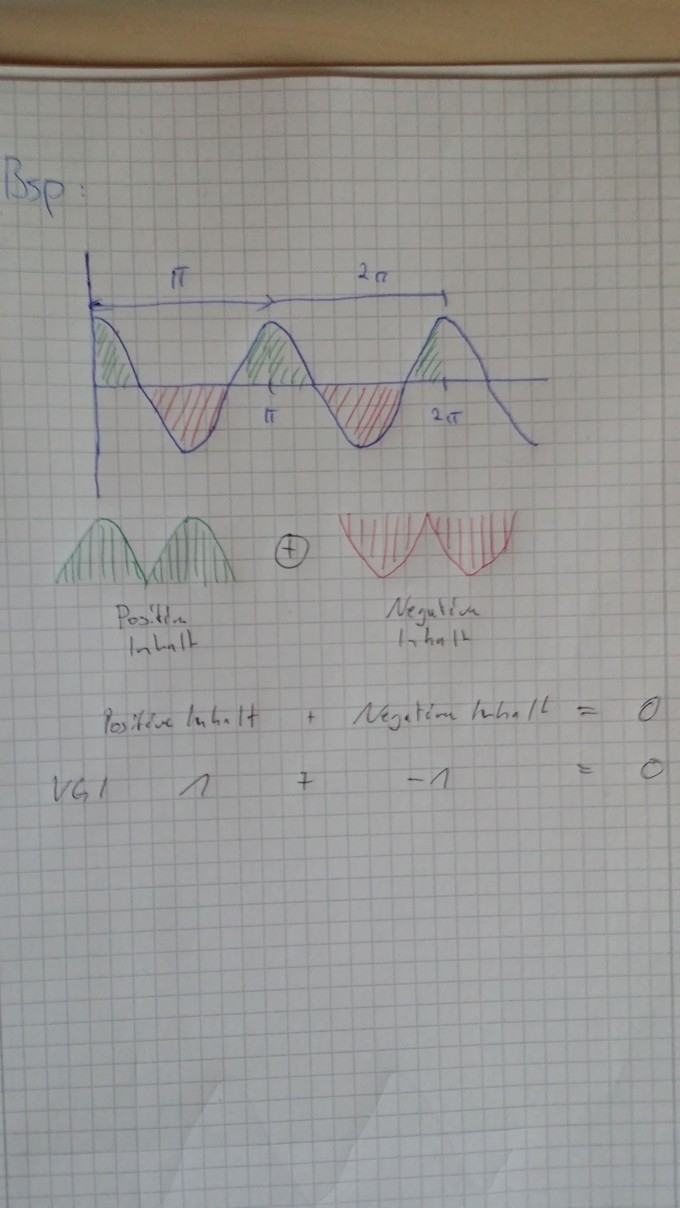
Genau genommen ist der Begriff Fläche auch nicht gut, bei Integralen, Funktionswerte wären besser...