Question

Das abgebildete Glücksrad (mit drei gleich großen Sektoren) wird zweimal gedreht.

Mit welcher Wahrscheinlichkeit

a) erscheint in beiden fällen Rot

b) erscheint mindesten einmal Rot

(Wie zeichne ich ein Baumdiagramm?)

Answer 1

Wir bekommen folgenden Baumdiagramm:

  

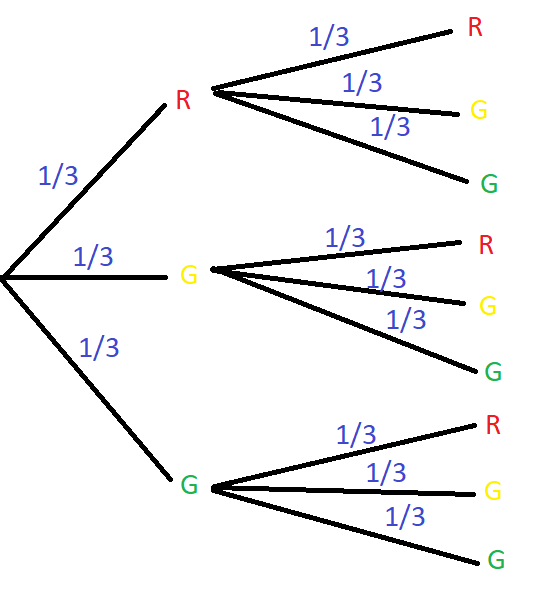
a) Laut der ersten Pfadregel gilt folgendes:

Die Wahrscheinlichkeit eines Elementarereignisses ist gleich dem Produkt der Wahrscheinlichkeiten des zugehörigen Pfades. 

Es gilt also dass $$\text{ P("zweimal rot") } =\frac{1}{3}\cdot \frac{1}{3}=\frac{1}{9}$$  

b) Hier kann man die Gegenwahrscheinlichkeit anwenden: $$\text{P("mindestens einmal rot") }  =1-\text{P("keinmal rot")}$$ oder auch folgendes berechnen: $$\text{P("mindestens einmal rot") }=\text{P(\{Rot, Rot\})}+\text{P(\{Rot, Grün\})}+\text{P(\{Rot, Gelb\})}+ \text{P(\{Grün, Rot\})}+\text{P(\{Gelb, Rot\})}$$

Answer 2

a:)
1/3 * 1/3 = 1/9

b.)
1Umdrehung Rot
1/3 * 2/3 = 2 / 9
2Umdrehung Rot
2/3 * 1/3= 2 / 9

2/9 + 2/9 = 4 / 9

Baumdiagramm kann ich leider nicht.

Comments

Nachtrag
2 mal Rot kann auch sein
1/3 * 1/3 = 1 / 9
4/9 +1/9 = 5/9

---

"2 mal Rot kann auch sein
4/9 +1/9 = 5/9 "

Kann nicht sein!

---

Und bei b) heißt es "mindestens einmal rot"