Extremalprobleme: Die dreieckige Rückwand eines Zeltes hat die Seitenlänge 2mx2mx2m.

Question

die Beziehung zwischen Mathe und mir ist bei einigen Teilen sehr gut und bei anderen Teilen führen wir leider Krieg! Darum hoffe ich das ihr mir helfen könnt. Damit ich eventuell mehr von den Thema hier verstehe!

Die Aufgabe lautet: Zelt
Die dreieckige Rückwand eines Zeltes hat die Seitenlänge 2mx2mx2m. Zur besseren Innenbelüftung soll ein rechteckiges Insektengitter eingenäht werden. Welche Breite und welche Höhe muss das Gitter erhalten, wenn sein Flächeninhalt maximal werden soll?

Mein Ansatz :

A=h⋅b Nebenbedingung

Answer 1

Zeichne eine Höhe in das gleichseitige Dreieck und lege den Fußpunkt F der Höhe so in den Ursprung, dass der Kopfpunkt K der Höhe auf der y-Achse liegt. Bezeichne den Eckpunkt des Dreiecks, der auf der positiven x-Achse zu liegen kommt, mit B.

Hier eine Skizze:

 

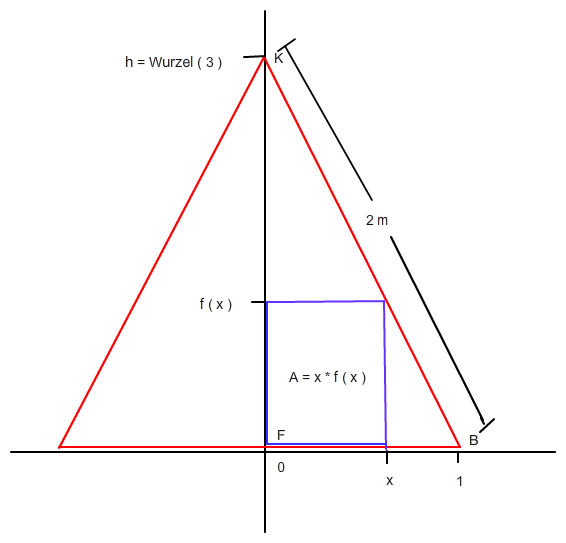
Betrachte nun nur die rechte Hälfte des Dreiecks, also das Dreieck KFB.

Die Höhe h = √ ( 3 ) dieses Dreiecks ergibt sich aus dem Satz des Pythagoras.

Die Seite BK dieses Dreiecks ist eine Gerade. Ihre Geradengleichung ist, wie man aus der Skizze ablesen kann:

f ( x ) = - √ ( 3 ) * x + √ ( 3 )

Maximiert werden soll die blau umrandete Fläche. Diese hat in Abhängigkeit von x den Flächeninhalt:

A ( x ) = x * f ( x ) = x * ( - √ ( 3 ) * x + √ ( 3 ) )

= - √ ( 3 ) x ² + √ ( 3 ) x

Die Ableitung von A nach x ist: 

A ' ( x ) = - 2 * √ ( 3 ) x + √ ( 3 )

Extremstellen liegen höchstens dort vor, wo die Ableitung von A den Wert Null annimmt, also:

A ' ( x ) = 0 

<=> √ ( 3 ) = 2 * √ ( 3 ) x

<=> 1 = 2 x

<=> x = 1 / 2

An der Stelle x = 1 / 2 liegt dann ein Extremwert vor, wenn die zweite Ableitung A ' ' ( x ) dort ungleich Null ist. Der Extremwert ist dann ein Maximum, wenn A ' ' ( x ) negativ ist, sonst ein Mnimum.

A ' ' ( x ) = - 2 * √ ( 3 )

A ' ' ( x ) ist also für alle x negativ, und damit insbesondere auch für x = 1 / 2. Also liegt bei x = 1 / 2 ein Maximum von A ( x ) vor.

Die Höhe des Rechtecks an der Stelle x = 1 / 2 ist:

f ( 1 / 2 ) = - √ ( 3 ) / 2 + √ ( 3 ) = √ ( 3 ) / 2

sodass für den maximalen Flächeninhalt der blau umrandeten Fläche gilt:

A ( x ) = x * f ( x ) = ( 1 / 2 ) * √ ( 3 ) / 2  = √ ( 3 ) / 4

Da nur die rechte Hälfte des Dreiecks betrachtet wurde, ist die Breite zu verdoppeln. Die gesuchte Breite beträgt also 1 m und die gesuchte Höhe √ ( 3 ) / 2 = 0,866 m (gerundet).

Ob es sinnvoll ist, das Insektengitter am Boden des Zeltes beginnen zu lassen, muss der Konstrukteur wissen.  Das größtmögliche Rechteck jedenfalls beginnt am Boden.

Comments

Viel Dank für die Antwort. Ich kam wirklich nicht klar.

Answer 2

Ich möchte noch einen alternativen Weg vorschlagen. Rechnerisch ist dieser ein kleines bisschen komplizierter, also würde ich im Nachhinein wohl auch JotEs Weg wählen. Vom Ansatz her gefiel mir meine Idee aber gut und da ich eh schon die Hälfte der Rechnung eingetippt hatte, um nach Hilfe bei der Suche nach meinem Fehler zu fragen, bevor ich ihn dann selbst gefunden habe, dachte ich, dass ich die Lösung doch auch gleich teilen könnte - insbesondere da die Aufgabe noch immer in den aktuellen Mathe Schulbüchern auftaucht :)

Hauptbedingung: $$A(b,h)=b \cdot h$$

Der 2. Strahlensatz liefert die Beziehung :

$$ \frac{b}{2} = \frac{2-x}{2} \quad \Leftrightarrow \quad b=2-x \quad \Leftrightarrow \quad x=2-b $$

Die unter Kante setzt sich aus drei Teilstücken zusammen:

$$ 2 = y+b+y=2y +b \quad \Leftrightarrow \quad y=1-\frac{b}{2} $$

Letztendlich lassen sich mit dem Satz des Pythagoras die Gleichungen zusammenführen:

$$ \begin{aligned} x^2 &= y^2 + h^2 \\(2-b)^2 &= \left( 1-\frac{b}{2} \right)^2  + h^2 \\4-4b+b^2 &= 1 - b +\frac{b^2}{4} +h^2 \\3-3b+\frac{3}{4}b^2 &= h^2 \\h &= \sqrt{\frac{3}{4}b^2-3b+3} \end{aligned} $$

Somit erhält man die Zielfunktion und kann nach etwas Umformen das Maximum bestimmen:

$$ \begin{aligned} &&A(b) &= b \cdot \sqrt{\frac{3}{4}b^2-3b+3} \\[12pt]&& &= b \cdot \sqrt{\frac{3}{4}\left(b^2-4b+4\right)} \\[12pt]&& &= b \cdot \sqrt{\frac{3}{4}\left(b-2\right)^2}\\[12pt]\text{Bemerkung: }&& \sqrt{x^2}= |x| \quad \land \quad b\le 2 \quad &\Rightarrow \quad \sqrt{\left( b-2\right)^2} = |b-2|=2-b\\[12pt]&& &= b \cdot\frac{\sqrt{3}}{2}\cdot\left(2-b\right) \\[12pt]&& A(b)&= \frac{\sqrt{3}}{2}\left(2b-b^2\right) \\[12pt]\text{Ableitungen:}&& A'(b) &= \frac{\sqrt{3}}{2}\left(2-2b\right) \\[12pt]&& A''(b) &= -\sqrt{3} \\[12pt]\text{Extrema:} && 0&=A'(b_E) \\[12pt]&& 0&=\frac{\sqrt{3}}{2}\left(2-2b_E\right) \\[12pt]&& b_E&=1 \\[12pt]&& A''(b_E)=-\sqrt{3}<0 \quad &\Rightarrow \quad \text{Hochpunkt bei }b_E=1 \\[12pt]\text{Einsetzen:} && h_E &= \sqrt{\frac{3}{4}\cdot 1^2-3\cdot 1+3} \\[12pt]&& &= \frac{\sqrt{3}}{2}\end{aligned} $$

Die Fläche ist also maximal bei einer Breite von 1m und einer Höhe von \(\frac{\sqrt{3}}{2}\)m

Answer 3

In Anbetracht der doch ellenlang geratenen Berechnungen
hier die etwas kürzere Variante

Rechte Seite der Zeltplane
2^2 = 1^2 + h^2
h = √ 3

2 Punkte
( 0 |  √ 3 )  ( 1 | 0 )

Geradengleichung

m = Δ y / Δ x = ( √ 3 - 0 ) / ( 0 - 1 )
m = - √ 3

y-Achsenabschnitt
b = √ 3

f ( x ) = - √ 3 * x + √ 3

A = x * f ( x  )
A = x * (  - √ 3 * x + √ 3 )
A =  - √ 3 * x^2 + √ 3 * x

1.Ableitung
A ´( x ) =  - √ 3 * 2 * x + √ 3

Extremwert bei
- √ 3 * 2 * x + √ 3  = 0
x = 1/2

Die Lösung entspricht auch den Erfahrungen bei denen
ein Rechteck in ein Dreick eingepaßt wird.
Der Extremwert ist immer die Stelle : x / 2