Extremalproblem. Ein Tunnel soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten. Wie groß..

Question

Ein Tunnel soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten. Wie groß ist die Querschnittsfläche maximal, wenn der Umfang des Tunnels 20m betragen soll?

Comments

Ich komme bei dieser Aufgabe nicht weiter haben erst eine Aufgabe zu diesem Themenkomplex gerechnet und ich habe keine Ahnung wie ich das machen muss. Ich hoffe es kann mir einer helfen.

---

Kannst du die Antwort hier an dein Tunnel anpassen? https://www.mathelounge.de/58617/gebrochenrationale-funktionen-querschnitt-aufgesetztem

---

Hmm ich habe mir die andere Aufgabe mal angeguckt doch leidee verstehe ich auch diese rechnung nicht, weil bei mir der umfang geben ist. Ich weiß also immer noch nicht was ich rechnen soll.

---

Vom Duplikat:

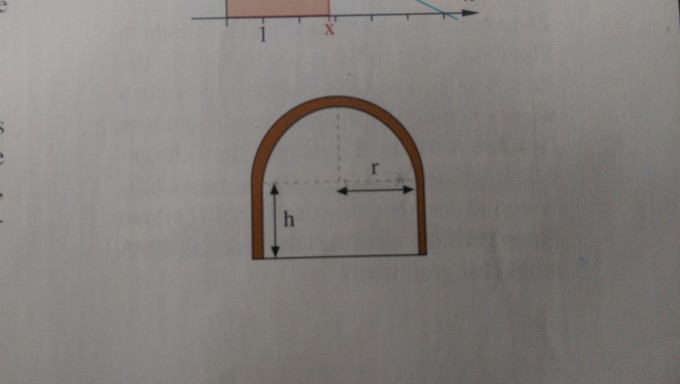
Titel: Extremalprobleme Ein Tunnel soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten

Stichworte: halbkreis,extremalproblem

Ein Tunnel soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten. Wie groß ist die querschnittsfläche maximal,

wenn der Umfang des Tunnels 20 m betragen soll?

Wir haben letzte woche mit dem neuen Thema extremalprobleme angefangen ich hatte auch bisher keine probleme

damit aber bei dieser Aufgabe bin ich überfragt weil der einzige gegebene Wert der Umfang ist und die form ein halbkreis

ich komme nicht weiter 

Hilfe wäre nett

LG Zino

---

Oder auf dieser Seite eine Frage tiefer unter
" Ähnliche Fragen ".

https://www.mathelounge.de/86223/extremalproblem-rechtecks-aufgesetztem-halbkreis-erhalten

Bei Bedarf  nachfragen.

Answer 1

Ein Tunnel soll die Form eines Rechtecks mit aufgesetztem Halbkreis erhalten. Wie groß ist die Querschnittsfläche maximal, wenn der Umfang des Tunnels 20m betragen soll?

Rechteck:

Breite: b

Höhe: a

Halbkreis:

r = b/2

Halber Umfang u_Kreis/2 = πr = πb/2

Nebenbedingung

u_Tunnel= 2a + b + πb/2 = 20

Soweit ok? Zeichne das mal. (folgt mehr)

2a = 20 -b(1 +π/2)

a = 10 - b(1+π/2)/2

Zielfunktion

A(b) = ab + 0.5π(b/2)^2

a einsetzen

= (10 - b(1+π/2)/2)b +  0.5π(b/2)^2

= 10b - b^2/2 - b^2 π/4 + b^2 π/8

= 10- b^2/2 - b^2*π/8

A'(b) =10  -b - bπ/4 =0

---> b=40/(4+π)

Stimmt nun mit WolframAlpha überein.

https://www.wolframalpha.com/input/?i=A%28b%29+%3D%2810+-+b%281%2Bπ%2F2%29%2F2%29b+%2B+π%28b%2F2%29%5E2%2F2

Berechne noch das zugehörige a und mach die Probe in der Nebenbedingung.

Comments

Wie berechne ich nun a und setzte das ein? Ich bin nämlich eine totale niete in mathe und habe selbst von formelnumstellen keine ahnung wenns komplizierter wird

---

Am besten hier:

a = 10 - b(1+π/2)/2

= 10 - 40/(4+π) (1+π/2)/2)

Versuch die Umformung selbst und kontrolliere damit: https://www.wolframalpha.com/input/?i=+10+-+40%2F%284%2Bπ%29+%281%2Bπ%2F2%29%2F2%29

Falls erlaubt, darfst du vielleicht auf 5 bedeutsame Ziffern runden und schon mit einem gerundeten b und dem Taschenrechner rechnen. 

---

Ich bin zwar kein Matheass; möchte somit diese Rechnung nicht in Frage stellen, da sie so gesehen korrekt ist, jedoch meine ich, dass

 U(Tunnel)=20= 2*a + pi*b/2 ist, da b hier die Grundseite darstellt. Somit findet "b" im Umfang keine Berücksichtigung, was parallel zu einer größeren Maximalfläche A führen würde.

Ist diese Überlegung korrekt?

---

@bh6055: Ich sehe deine Frage erst jetzt. Umfang ist ein mathematischer Begriff und hier auch als solcher zu interpretieren. Vgl. Link in der Antwort von Grosserloewe, die zu diesem Übungsblatt inkl. Lösung führt. 

http://www.gxy.ch/6gfpam/diff2/extremwertaufgaben-pvor.pdf

Answer 2

siehe hier: (2.Aufgabe)

http://www.gxy.ch/6gfpam/diff2/extremwertaufgaben-pvor.pdf