Meine Frage bezieht sich auf eine Beispielaufgabe aus einem Buch:
Es wird die Potenzreihe
P(x)=∑n=0 bis ∞ (xn) = 1+ x + x2 + x3 + ... = 1 / (1-x)
abgeleitet zu:
P'(x)=∑n=0 bis ∞ ((n+1)xn) = 1+ 2x +3x2 + 4x3 + ... = 1 / (1-x)2
Nun sehe ich ein das die rechte Seite über die Kettenregel abgeleitet stimmt, allerdings verstehe ich leider nicht wie der Author von
xn zu (n+1)xn kommt
Meiner Auffassung nach müsste dort ja ganz einfach
n*xn-1 rauskommen
nicht nur wegen der Ableitungsregel, auch von den Summenwerten her macht das andere nicht recht Sinn ohne den Anfangswert von n zu versetzen oder ähnliches, was allerdings nicht getan oder erwähnt wird.
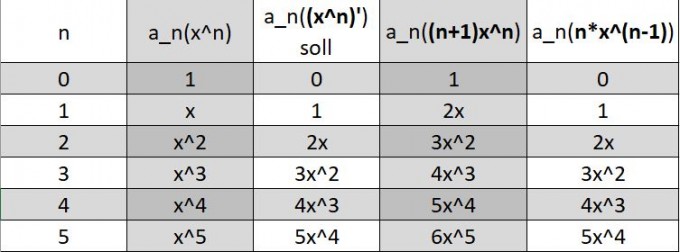
Hier noch eine Tabelle mit den Werten für die jeweiligen Funktionen, hoffe dass das mein Problem etwas besser verdeutlicht.