Es geht um die Länge der Strecke \(PQ\). Die Funktionen anzuschauen war bereits eine gute Entscheidung. Unten siehst Du sie nochmal ..
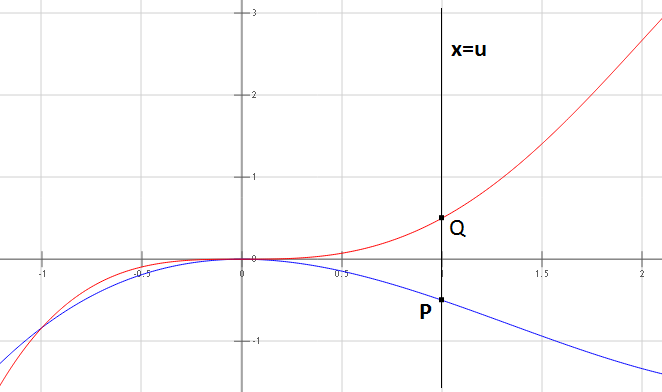
.. zusätzlich habe ich zwei Punkte an der Stelle \(x=1\) eingezeichnet. Dies sind die beiden Punkte \(P\) und \(Q\) an der Stelle \(x=1\). Eine Gerade mit der Gleichung \(x=u\) ist eine Gerade, die parallel zur Y-Achse verläuft und alle Punkte auf dieser Gerade haben den gleichen X-Wert, der hier als \(u\) bezeichnet wird.
Die Länge der Strecke \(PQ\) ist nun nichts anderes als die Differenz der beiden Funktionswerte von \(f(x)\) und \(g(x)\) an der Stelle \(x=u\), wobei sich \(u\) nur im Intervall von -1 bis 2 bewegen soll. Demnach ist \(|PQ|\):
$$|PQ|= \frac{1}{6}u^2(u-4) + \frac{1}{6}u^3(u-4)= \frac{1}{6}u^2(u-4)(1+u)$$
Ableiten ergibt (ich gehe davon aus, dass Du weißt wie das geht - sonst bitte nachfragen):
$$\frac{ \text{d} |PQ| }{\text{d}u}= \frac{1}{6}u(4u^2-9u-8)$$
daraus folgen die drei Extrema \(u_1=0\) und \(u_{2,3}=\frac{1}{8}(9 \pm \sqrt{209})\). Wobei \(u_2 \approx 2,93\) außerhalb des Intervalls \([-1;2]\) liegt. Bleiben \(u_1=0\) (ein lokales Minimum) und \(u_3\approx -0,6821\) (ein lokales Maximum) über. Ein Blick auf die Funktionen zeigt, dass dies Sinn macht.
Bleiben noch die absoluten Extrema. Da genügt ein Blick auf die Graphen. Ein absolutes Maximum liegt bei \(u=2\) und bei \(u=-1\) liegt ein zweites Minimum mit \(|PQ|=0\). Wie lang die Strecke \(PQ\) dort ist, kannst Du jetzt bestimmt selbst berechnen ;-)
Falls Fragen offen sind, bitte melden.
Gruß Werner