Löse durch Substitution

Question

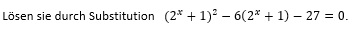
Ich komme bei der Aufgabe nicht weiter. Meine Idee war, für 2^x=u einzusetzen.

Jedoch, komme ich so nicht auf die Lösungsmenge von 3.

Als zweites, habe ich alles ausmultipliziert und zusammen gerechnet, wodurch ich auf

2^2x-2^3x-32=0

kam.

Scheint aber auch nicht richtig zu sein weil ich da nichts substituieren kann.

Answer 1

Hi,

Substituiere

2^x + 1 = u

u^2 - 6u - 27 = 0   |pq-Formel

u_(1) = -3 und u_(2) = 9

Resubstitution

2^x+1 = -3   |-1

2^x = -4

Geht nicht, da 2^x stets positiv ist.

2^x + 1 = 9   |-1

2^x = 8 = 2^3

x = 3

Wir haben die Lösung x = 3 für obiges Problem.

Grüße

Answer 2

( 2^x + 1 )^2 - 6 * ( 2^x + 1 ) - 27 = 0
Kann man auch so ausrechnen.
Einfacher und übersichtliches wirds durch
die Ersetzung
a = ( 2^x + 1 )
a^2 - 6 * a - 27 = 0
pq-Formel oder quadratische Ergänzung
a^2 - 6a + 3^2 = 27 + 3^2
( a - 3 )^2 = 36
a - 3 = ± 6
a = 9
oder
a = -3

Rückersetzen
a = ( 2^x + 1 )
9 = ( 2^x + 1 )
2^x = 8  | ln
x * ln(2) = ln(8)
x = ln(8) / ln(2)
x = 3

und
-3 = ( 2^x + 1 )
2^x = -4
keine Lösung