Obersumme für n=100 von f(x) = x ^4 / 6 berechnen

Question

Ich habe eine Funktion f(x) = x ^4 / 6, die im Intervall [0;4] in 100 Rechtecke geteilt werden soll.  Mit der Summenformel n^2*(n+1)^2/4 soll ich die Obersumme bilden. Wie muss ich in diesem Fall vorgehen?  Wäre sehr dankbar für eure Antworten.

Liebe Grüße aus Berlin von Volker!

Answer 1

Hi,

die Obersumme sieht in diesem Fall so aus
$$ \Delta \sum_{1=1}^N f(x_i) $$ mit \( \Delta = \frac{4}{N} \) und \( N = 100 \) sowie \( f(x) = \frac{x^4}{6} \) und \( x_i = i \cdot \frac{4}{N} \)

Weil $$ \sum_{i=1}^N i^4 = \frac{N(N+1)(2N+1)(3N^2+3N-1)}{30} $$ gilt

siehe http://www.arndt-bruenner.de/mathe/Allgemein/summenformel2.htm
folgt, wenn man die Terme \( \frac{1}{N} \) vernachlässigt
$$  \Delta \sum_{1=1}^N f(x_i) \approx \frac{2^{10}}{N} $$

Comments

Ich denke, das Ergebnis von Gorgar und mir ist richtig:

₀∫⁴  x⁴ / 6   dx  ≈  34,13333333  

und das weicht doch deutlich ab von    2¹⁰ / 100 = 10,24

Answer 2

Hallo Volker! :-)

Wir können für die Berechnung der Obersumme die Formel \( \bar{S_n} = \frac { b - a}{ n } \sum_{i=1}^{n}{f \left( a + \frac { i(b-a) }{ n }\right)} \) benutzen. Mit \( a=0 \), \(b=4 \) und \(n=100\) bekommen wir $$ \bar{S}_{100} = 0,04\sum_{i=1}^{n}{f\left(i\cdot 0,04\right)}= 0,04\sum_{i=1}^{n}{\frac { (i\cdot 0,04)^4 }{ 6 }}= \frac { 0,04^5 }{ 6 }\sum_{i=1}^{100}{i^4} = \\ \frac { 0,04^5 }{ 6 } \cdot 2050333330 \approx \underline{\underline{34,99}}. $$

Die Summe \( \sum_{i=1}^{n}{i^4} \) lässt sich mit \(\sum_{i=1}^{n}{i^4} = \frac{1}{30}n (n + 1) (2 n + 1) (3 n^2 + 3 n - 1) \) https://www.wolframalpha.com/input/?i=sum+i%5E4,+i%3D1+to+n durch Einsetzen von \( n = 100 \) oder doch lieber einfacher mit https://www.wolframalpha.com/input/?i=sum+i%5E4,+i%3D1+to+100 berechnen.

Beste Grüße 
gorgar

Answer 3

Hallo Volkert,

da  f auf  [0 ; 4]  streng monoton steigend ist, ist die folgende Skizze brauchbar:

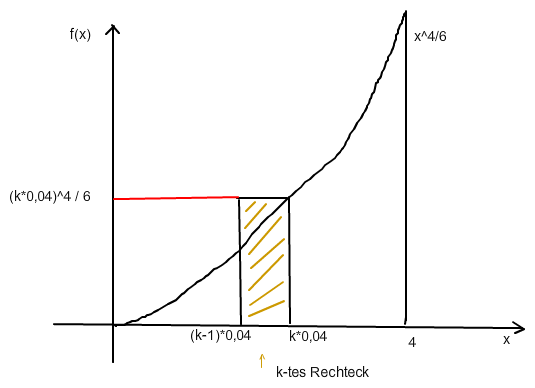
das k-te Rechteck dieser Obersumme hat die Breite 4/100 und die Höhe (k*0.04)^4 / 6 und damit die Fläche  0.04 *  (k * 0.04)^4 / 6  =  0.04 * 0.04⁴ / 6 * k⁴  = 0.04⁵/6 * k⁴.

Obersumme  =  0.04⁵/6 * \(\sum\limits_{k=1}^{100} k^4\)  =  0.04⁵/6 * 2050333330  ≈  34.992   

 [   \(\sum\limits_{k=1}^{n} k^4\)  =  1/30 * n * (n+1) * (2n+1) * (3n² + 3n - 1)  mit n=100. 

    Deine Summenformel \(\sum\limits_{k=1}^{n} k^3\) =  n²*(n+1)²/4  könntest du z.B. bei  f(x) = x³/6  verwenden

           Die Summenformeln findest du unter 

           http://www.arndt-bruenner.de/mathe/Allgemein/summenformel2.htm  ]  

Gruß Wolfgang