Anwendungen der Integralrechnung, Flächeninhalte berechnen

Question

Könnte mir jemand helfen, ich kenne mich nicht aus.

Answer 1

Hallo JB,

Am übersichtlichsten vertauschst du wohl die Variablennamen  x ↔ y  (Siegelung an der 1.Winkelhalbierenden)

x² = 3y   →   y = 1/3 x²

x² = 9/2 * (y-1)  →  y = 2/9 x² + 1  

 

und gehst dann wie gewohnt vor: 

Schnittstellen:   1/3 x² = 2/9 x² + 1   ⇔  1/9 x² = 1  ⇔   x² = 9  ⇔  x = ± 3

Wegen der Achsensymmetrie gilt

A = 2 * ₀∫³ ( 2/9 x² + 1 - 1/3 x² )  dx   =   2 * ₀∫³ ( -1/9 x² + 1 )  dx   

    = 2 * [ - x^3/27 + x ]  = 2 * 2  = 4 

Gruß Wolfgang

Answer 2

umgestellt nach y bzw. f ( x ) / g ( x )

f ( x ) = √ ( 3 * x ) = ( 3 * x )^{1/2}
g ( x ) = √ ( 9/2 * ( x -1 ) ) = ( 9/2 * ( x -1 )) ^{1/2}

Die Skizze zeigt dir

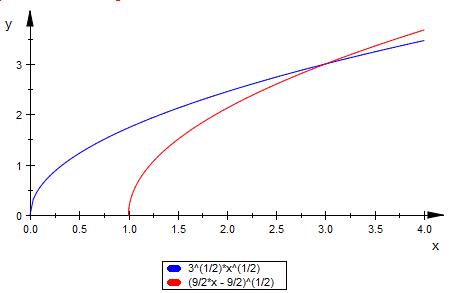Der Schnittpunkt ist
f ( x ) = g ( x )
√ ( 3 * x ) = √ ( 9/2 * ( x -1 ) )
( 3 * x ) = 9/2 * ( x - 1 )
3x - 4.5x = . 4.5
x = 3

Es wird jetzt abgezogen
Die Fläche unterhalb der roten Kurve g ( x ) von 1..3
von der blauen Kurve f ( x ) von 0..3

Stammfunktionen
f ( x ) = ( 3 * x )^{1/2}
f ( x ) = 3^{1/2} * x^{1/2}
F ( x ) =   3^{1/2} * x^{1/2}
F ( x ) =   3^{1/2} * 2/3 * x^{3/2}

g ( x ) = ( 9/2 * ( x -1 ) )^{1/2}
G ( x ) = 9/2^{1/2} * 2/3 * ( x -1 )^{3/2}
G ( x ) = 2^{1/2}  * ( x -1 )^{3/2}

Flächen
[ F ( x  ] zwischen 0 und 3
3^{1/2} * 2/3 * ( 3^{3/2} - 0^{3/2 } )
6

[ G ( x ) ]  zwischen 1 und 3
2^{1/2}  * [ ( 3 -1 )^{3/2} - ( 1 -1 )^{3/2} ]
4

6 - 4 = 2

Alles ein bißchen aufwendig.
Bei Bedarf nachfragen.