Hallo Sanny,
zunächst mal zum Inhalt: Quadratische Ergänzung
da hätte ich zwei Ideen: 1.) Du könntest Deinen Mitschülern Aufgaben vorstellen, die zunächst leicht und dann immer schwerer zu lösen sind. Binde deine Zuhörer mit ein - lasse sie die Aufgabe lösen - etwa so:
$$x^2= 4$$
... ist klar oder
$$x^2=6$$
die korrekte Lösung(en) wäre \(x_{1,2}\pm\sqrt{6}\) - hier gibt es keine Dezimalzahl mit endlicher Anzahl von Stellen, mit der man die Lösung exakt darstellen kann.
$$(x+2)^2=6$$
wie oben oder? ... nur nach dem Wurzelziehen noch mit \(-2\) angehängt.
$$x^2+6x+9 = 6$$
jetzt wird es schwieriger. Die Kenntnis der binomischen Formeln ist von Vorteil \(x^2+6x+9=(x+3)^2\) .. und dann geht es wie schon vorher weiter. Ja - und schlussendlich
$$x^2+12x+27=0$$
Lasse Deine Zuhörer darauf kommen, dass man 9 addieren muss, damit aus \(x^2+12x+36\) das Quadrat \((x+6)^2\) machen kann. Falls niemand drauf kommt, so frage sie konkret, welchen Wert man addieren muss, um auf die binomische Formel zu kommen.
2.) ziehe das ganze graphisch auf: Beginne mit einem Quadrat mit der Seitenlänge \(x\) dessen Fläche \(=36\) ist. Zeichen das Quadrat hin und benenne die Seiten mit \(x\). Frage nach, wei groß \()x\) sein muss, um auf die gewünschte Fläche zu kommen.
Nächster Schritt: Zeichne ein Rechteck mit den Seitenlängen \(x\) und \(x+4\) welches einen Flächeninhalt von 21 haben soll. Und behaupte anschließend, dass sich die Aufgabe lösen lässt, wenn auf einer Seite ein Quadrat steht - nur dann kann man die Wurzel ziehen:
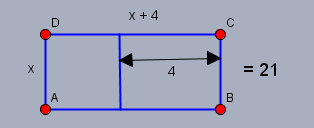
auf dem Weg zum Quadrat halbiere den Rechten Teil des Rechtecks und 'klebe' eine Hälfte um \(90°\) unten wieder dran. Sieht so aus:
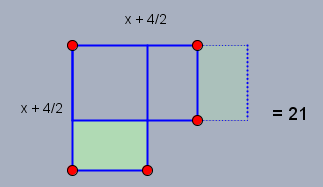
Im letzten Schritt 'addierst' Du auf beiden Seiten der Gleichung das fehlende Quadrat \(2\times 2\) unten rechts auf der linken Seite und Du erhältst \((x+2)^2=25\). Die Lösungen wären hier \(x_1=3\) und \(x_2=-7\) - als Bonbon kannst Du deine Mitschüler nun fragen, wie man die zweite Lösung \(x_2=-7\) graphisch interpretieren kann. Dazu folgende Zeichnung
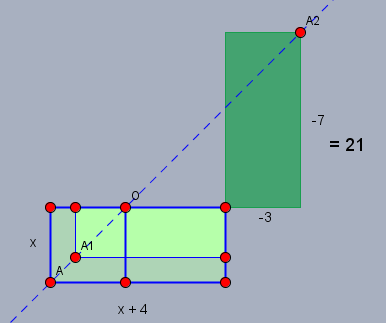
Im Punkt \(A\) hat das Rechteck die Fläche \(21\) und \(x=3\). Verkleinert man nun den Wert von \(x\), so wandert der Punkt auf der gestrichelten Linie nach rechts oben - z.B. nach \(A_1\) mit \(x=2\). Erreicht \(A\) den Punkte \(O\), so ist \(x=0\) und die Fläche wird zu \(0\). Wandert der Punkt weiter und erreicht \(A_2\), so ist \(x=-7\) und die Fläche ist wieder \((-7+4)\cdot(-7)=21\).
Zu der Verschiebung würde ich Dir das Vorgehen empfehlen, wie in meiner Antwort. Das Entscheidende ist wohl, dass Du bei einer Verschiebung um \(+1\) immer von \(y^*=y+1\) bzw. \(x^*=x+1\) ausgehst. Und anschließend formst Du die Ausdrücke in \(y=y^*-1\) bzw. \(x=x^*-1\) um und setzt sie in die zu verschiebende Funktion ein.
Nochmal zur Präsentationstechnik: Du kannst alles oben beschrieben auch gut an der Tafel mit Kreide (und Schwamm) entwickeln - wenn Du mit Folien auf Overheadprojektor keine Erfahrung hast, so musst Du das mindestens vorher einmal üben, bevor Du damit auf die Menschheit los gehst. Übe auf jeden Fall den Vortrag vorher, nehme Deine Eltern, Geschwistern, Kumpel als Zuhörer. Du solltest vorher wissen wie viel Zeit Du benötigst. Es dauert meistens länger als Du denkst.
Schau Deine Zuhörer an - schaue alle an, nicht nur Deinen besten Kumpel in der ersten Reihe. Das was Du sagst und gerade zu sehen ist, muss das selbe sein - so prägt es sich am besten ein. Stelle Fragen (s.o.) auch wenn Du gleich die Antwort selber gibst. So sicherst Du Dir die Aufmerksamkeit Deiner Zuhörer/-seher. Da gibt es noch einige Tipps - kannst ja mal im I-Net suchen ...
Ansonsten viel Erfolg - und frage hier ruhig nochmal nach, wenn Dir danach ist
Gruß Werner