Quadratische Funktionen notieren

Question

Aufgabe:

a) notieren Sie die Funktionsgleichungen

b) Zeichnen Sie den Graphen folgender Funktion in das Koordinatensystem ein: k(x) = 2(x+2)^2 +1

c) formen Sie die Parabelgleichungen in die Normalform um

Problem/Ansatz:

Ich benötige Hilfe und würde mich sehr über eine Antwort freuen, damit ich den Lösungsweg verstehen und auf andere Aufgaben anwenden kann. Ich wäre sehr dankbar.

Text erkannt:

1 In Abbildung 1 sind die Graphen verschiedener Funktionen dargestellt.

Answer 1

Hallo,

die Scheitelpunktform einer quadratischen Funktion lautet \(f(x)=a(x-d)^2+e\) mit dem Scheitelpunkt S (d|e).

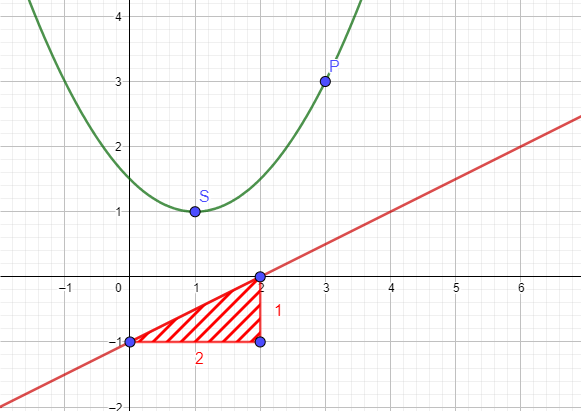
Der Scheitelpunkt des Graphen von g ist S (1|1). Setze die Koordinaten in die Funktionsgleichung ein.

\(f(x)=a(x-1)^2+1\)

Wähle einen weiteren, gut ablesbaren Punkt, hier z.B. P (3|3) und setze seine Koordinaten ebenfalls in die Gleichung ein, um a zu bestimmen.

\(3=a(3-1)^2+1\\ 3=4a+1\\ a=\frac{1}{2}\)

Damit lautet die Funktionsgleichung \(f(x)=\frac{1}{2}(x-1)^2+1\).

Für die Normalform multiplizierst du die Klammer mit Hilfe der 2. Binomischen Formel aus und fasst zusammen:

\(f(x)=\frac{1}{2}(x-1)^2+1\\ =\frac{1}{2}(x^2-2x+1)+1\\ =\frac{1}{2}x^2-x+0,5+1\\ =\frac{1}{2}x^2-x+1,5\)

Für den Graphen von f gehst du genauso vor.

h ist eine Gerade. Die allgemeine Form einer Geradengleichung ist y = mx + b mit

m = Steigung, b = Schnittpunkt mit der y-Achse.

y = mx - 1

Um m zu bestimmen, kannst du ein Steigungsdreieck einzeichnen oder du wählst zwei Punkte, und setzt ihre Koordinaten in die Formel \(m=\frac{y_1-y_2}{x_1-x_2}\) ein.

Melde dich, falls du noch Fragen hast.

Gruß, Silvia

Comments

Vielen lieben Dank für Ihre Hilfe! Das hat mir sehr weitergeholfen.

Answer 2

Scheitelpunktform. Die Funktion

      \(f(x) = a(x-d)^2 + e\)

hat den Scheitelpunkt bei \((d|e)\). Dass musst du auswendig wissen.

Nachdem du damit \(d\) und \(e\) bestimmt hast, setzt du einen Punkt der Parabel in die Funktionsgleichung ein und löst die Gleichung.

a) Beispiel. Eine Parabel hat den Scheitelpunkt \((-3|7)\) und verläuft durch den Punkt \(P=(1|-1)\).

Aufgrund des Scheitelpunktes ist

        \(f(x) = a(x+3)^2 + 7\).

Einsetzen von \(P\) liefert

        \(-1=a(1+3)^2 + 7\)

also \(a = -\frac{1}{2}\) und somit

        \(f(x) = -\frac{1}{2}(x+3)^2 + 7\).

b) Scheitelpunkt bestimmen, Wertetabelle um den Scheitelpunkt herum bestimmen. Punkte einzeichnen. Kurve durch die Punkte zeichnen.

c) Beispiel.

        \(\begin{aligned} f(x) & =-\frac{1}{2}(x+3)^{2}+7 &  & \text{bin. Formeln}\\ & =-\frac{1}{2}(x^{2}+6x+9)+7 &  & \text{ausmultiplizieren}\\ & =-\frac{1}{2}x^{2}-3x-\frac{9}{2}+7 &  & \text{zusammenfassen}\\ & =-\frac{1}{2}x^{2}-3x+\frac{5}{2} \end{aligned}\)