Hallo Gast eg5999! :-)
In meinem Mathebuch verstehe ich nicht mal im Ansatz, warum das gemacht wird.
Die Entdeckung der Normalverteilung liegt lange vor dem Zeitalter der Computer. Früher gab es keine Computer - weder in privaten Haushalten, noch in Firmen, auch nicht an den Universitäten.
Funktionen der Normalverteilungen, deren Graphen Formen der Gaußschen Glockenkurven haben, lassen sich ohne Rechner nur mühsam integrieren. Statistik wurde früher ohne Computer betreiben und irgendwann hatte jemand die Idee der Standardisierung(Wer es war, konnte ich leider nicht im Internet recherchieren).
Jedenfalls wurde, mit der Methode der Standardisierung, mit Hilfe der Tabelle der Standardnormalverteilung, eine enorme Vereinfachung geschaffen, Integrale unter den unzählbar vielen verschiedenem Formen der Glockenkurven zu berechnen. Heute können wir die Integrale auch ohne Tabellen mit Hilfe des PC berechnen.
Beispiel: Normalverteilung: f(x) mit µ = 10 und σ = 2.
Wie viel Prozent aller Werte liegen in 5 <= x <= 12 ?
Berechnung durch Integration der Normalverteilungsfunktion https://www.wolframalpha.com/input/?i=integrate+1%2F(sqrt(2*pi)+*+2)e%5E(-(x-10)%5E2%2F(2*2%5E2)),+from+x+%3D+5+to+12
Berechnung durch Integration der z-Transformierten https://www.wolframalpha.com/input/?i=integrate++1%2Fsqrt(2*pi)*e%5E(-1%2F2*z%5E2)+from+z+%3D+-2.5+to+1
Das kann sogar ein handelsüblicher Taschenrechner für Schüler
Ich verstehe diesen Prozess nicht, bei dem man die Kurve so verstellt, dass der Erwartungswert bei x=0 liegt und die daraus resultierende Funktion.. Die Kurve wird nicht wirklich verstellt und der Erwartungswert bleibt auch wo er ist.(*)
Der Flächeninhalt unter der Kurve der Standardnormalverteilung ist wie auch der Flächeninhalt unter jeder beliebigen Kurve einer Normalverteilung gleich 1. Bei der Standardisierung(oder auch z-Transformation) wird ein z-Wert der Standardnormalverteilung ermittelt, der einem x-Wert einer bestimmten Normalverteilung entspricht.
Konkretes Beispiel(wie oben):
Normalverteilung: f(x) mit µ = 10 und σ = 2.
Wie viel Prozent aller Werte liegen in 5 <= x <= 12 ?
Gesucht ist also zunächst z1 für x = 5 und z2 für = 12
z1 = (x - µ) / σ = (5-10)/2 = -2,5
z2 = (x - µ) / σ = (12-10)/2 = 1
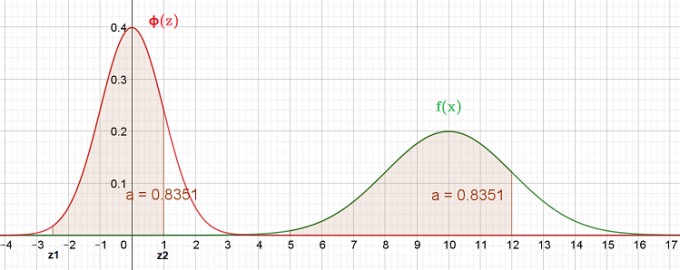
Mit z1, z2 haben wir die Intervallgrenzen der Standardnormalverteilung φ(z) ermittelt.
In diesem Intervall ist der Flächeninhalt unter der Kurve von φ(z) genauso groß, wie der Flächeninhalt im Intervall 5 <= x <= 12 unter der Kurve von f(x), nämlich: A = φ(1) - (1 - φ(2.5) = 0,84134 - (1 - 0,99379) ≈ 0,8351.
Das haben wir berechnet, ohne f(x) integrieren zu müssen! :-O Das die Flächen gleich sind, lässt sich durch den Vergelich der Reihenentwicklungen beider Integrale nachweisen.
(*)
Stell Dir zwei Glockenkurven vor, welche jeweils die Normalverteilung der Körpergrößen von Frauen und Männern repräsentieren. Bei einem Erwartungswert von Null würden wir alle recht platt durch die Gegend laufen! :-P
Hier findest Du weitere Infos
Ich hoffe, dass Ihr etwas Licht ins Dunkle bringem könntIch hoffe, es ist nun etwas heller geworden!
Beste Grüße
gorgar