Funktionsterm einer ganzrationalen Funktion 3. Grades

Question

Wer kann mir möglichst schnell helfen; Aufgabe ist:

Gesucht ist der Funktionsterm einer ganzrationalen Funktion 3.Grades mit folgenden Eigenschaften:
a) HP(3/2 ist Hochpunkt von G(f)
b) G(f) schneidet an der Stelle  x= -2 die Gerade g:y=0,5x + 2 senkrecht

Vielen Dank

Answer 1

Hallo ID,

f(x) =  a·x³ + b·x² + c·x + d

f '(x) = 3·a·x² + 2·b·x + c

g(x) = 0,5·x + 2

du hast vier Bedingungen für 4 Unbekannte:

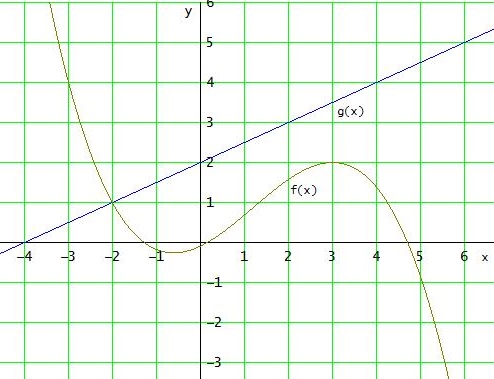
G_f verläuft durch (3|2):

f(3) = 2               ⇔   27·a + 9·b + 3·c + d = 2

Die Steigung im Hochpunkt (3|2) von G_f  ist gleich 0:

f '(3) = 0              ⇔   27·a + 6·b + c  =  0   

G_f  und G_g   schneiden sich an der Stelle  x = -2

f(-2) = g(-2)         ⇔  - 8·a + 4·b - 2·c + d  =  1  

Die Steigung m_f  von G_f  an der Stelle x = - 2  ist gleich  -1/m_g  

f '(-2) = -1/0,5 = - 2     ⇔   12·a - 4·b + c  =  -2

Das lineare Gleichungssystem kannst du ja wohl lösen.

(wenn du z.B. G2 - G4 rechnest, hast du ein 2x2-LGS für a und b. Nach deren Einsetzen noch einmal ein 2x2-LGS für c und d )

Das Kontrollergebnis   f(x)  =  - 12/125·x³ + 43/125·x² + 66/125·x - 11/125   kannst du hier

http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

berechnen lassen

Gruß Wolfgang