Aufgaben für Zwischentest (Funktionen/Differenzieren/etc)

Question

Ich hab Mitte November einen Zwischentest und da ich mir gerade alles irgendwie selber beibringen muss, hab ich ein mega Problem mit der Fragestellung der Aufgaben! 

Ich kann im ersten Moment leider gar nicht rauslesen auf was es ankommt und überhaupt wie ich die Fragen dann angehen soll. Mathe liegt bei mir leider ein bisschen zu weit zurück! 

Aber vll kann mir jemand helfen und versteht die Fragen und die Ausarbeitung?!

Zwischentest Fragen.pdf (0,3 MB)

Liebe Grüße,

Nadine 

Answer 1

Zu 1) Schau dir nochmal an, wie man den Vektor von einem Punkt zum anderen bestimmt und die Länge von Vektoren.

Dann brauchst du vielleicht noch das Skalarprodukt zur Winkelberechnung.

zu 2) Für die Tangete bedenke: Die Tangente ist eine Gerade, hat also eine

Gleichung der Art    y = mx+n .  Und m = f ' (x) wenn x die x-Koordinate

des Punktes ist, an dem die Tangente den Graphen berührt.

Bei x löse die Klammern auf, dann findest du leichter eine Stammfunktion.

Mit der berechne das Integral von 4 bis 7, dann hast du den gesuchten

Flächeninhalt.

Extrempunkte findet man mittels f ' (x) = 0.

Diese vergleiche mit den Werten am Rande des Definitionsbereiches.

Comments

OK vielen dank! 

Das hilft mir schon mal das Wichtigste rauszufiltern :)

Alles andere muss ich mir e noch genauer ansehen! Aber danke für die schnelle Antwort!

Lg Nadine 

Answer 2

Aufgabe 2)

                        

Answer 3

Hallo Nadine! :-)

Bsp3)

Für diese Aufgabe brauchst Du die Integralrechnung.
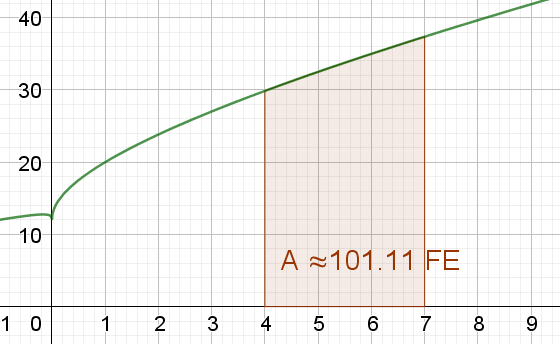
Der Flächeninhalt unter dem Graphen von f soll im Intervall [4, 7] berechnet werden(siehe Bild). Der zusätzliche Hinweis 0 ≤ y ≤ f(x) soll aussagen, dass f in dem Intervall [4, 7] keine Nullstellen hat, die man beachten muss. Multipliziere die Klammern aus: f(x) = (x^{3 / 5} + 4) (x^{2 / 5} + 3) = 3 x^{3/5} + 4 x^{2/5} + x + 12. Das lässt sich nun leicht mit der Summenregel der Integration integrieren. Um die Stammfunktion zu bekommen, integriere also die einzelnen Summanden mit der Potenzregel der Integration, setze die gegebenen Grenzen des Intervalls ein und berechne die Fläche.

Bsp4)

Für diese Aufgabe brauchst Du die Differentialrechnung. Bilde die erste Ableitung f ' von f, um die Minima und Maxima bestimmen zu können. Dafür würde ich die Klammern durch Ausmultiplizieren auflösen, dann lässt sich die Ableitung eventuell etwas leichter berechnen. Du brauchst hier die Summenregel, die Produktregel und die Kettenregel. Wenn Du die erste Ableitung bestimmt hast, setzte sie Null, denn an der Stelle x₀ ist ein Extremum(ein Minimum oder ein Maximum), wenn die erste Ableitung Null ist, wenn also f '(x₀) = 0 gilt(siehe Bild). Du brauchst also die Nullstellen von f '(x₀) = 0 im gegebenen Intervall [-1, 2] (hier gibt es nur eine). Wenn Du die Nullstelle hast, kannst Du mit der zweiten Ableitung oder dem Vorzeichenwechselkriterium bestimmen, ob es ein Minimum oder ein Maximum ist. Ich würde das Vorzeichenwechselkriterium wählen.

 

Ich hoffe nun ist Dir etwas klarer, wie Du die Fragen bearbeiten kannst!
Viel Erfolg!