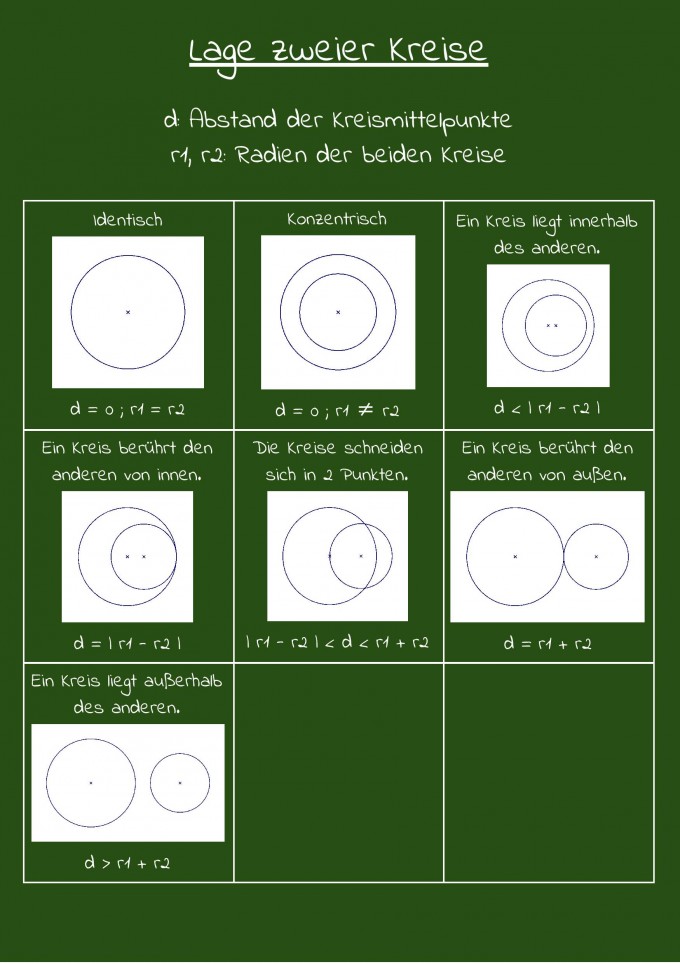
- dass wenn der Abstand der zwei Mittelpunkte kleiner als eins der beiden Radien ist, dass der eine Kreis vollständig in dem anderen (ohne dass sie sich berühren)?
Der Abstand der Mittelpunkt müsste kleiner sein als der Betrag der Differenz der Radien der Kreise.
- wenn die Summe der Radien kleiner ist als der Abstand der Mittelpunkte, dann haben die beiden Kreise keine Beziehung zu einander.
Das trifft so zu.
- und wenn die Summe der Radien ≥ Abstand der Mittelpunkte, dann schneiden bzw. berühren sich diese.
Betrag der Differenz der Radien <= Abstand der Mittelpunkte <= Summe der Kreisradien
Siehe dazu auch