tan(α'') = y / 0,4
y = 0,4 · tan(α'')
y(α) = 0,4·tan(90° - 2α)
Für 0 < x < 90° ist tan(x) > 0
Für -90° < x < 0 ist tan(x) < 0
y(α) > 0 für 0 < α < 45°
Wir wollen, dass y(α) links vom Ursprung < 0 ist, darum schreiben wir
y(α) = -0,4·tan(90° - 2α) oder
y(α) = -cot(2α)
b)
y(α) = -0,4/tan(2α), 0 ≤ α < 45°, 45° < α ≤ 90° oder
y(α) = -0,4·cot(2α), 0 < α < 90° daher wählen wir besser für die weitere Rechnung
y(α) = -0,4·cot(2α)
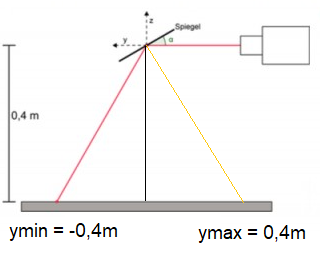
ymax = 0,4m
ymin = -0,4m
1) -0,4·cot(2α) ≤ 0,4 ⇒ α ≥ -π/8
2) -0,4·cot(2α) ≥ -0,4 ⇒ α ≤ π/8
-π/8 ≤ α ≤ π/8
Probe
α = π/8
y(π/8) = 0,4 cot(2(π/8)) = 0,4
α = -π/8
y(-π/8) = 0,4 cot(2(-π/8)) = -0,4
Passt - Juppieeee! :-)
:-O