Kurvendiskussion von f(x) = -5x^3·exp(4x+5).

Question

könnte mir bitte jemand bei dieser Aufgabe helfen?

Gegeben ist die Funktion f(x) = -5x^3·exp(4x+5).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a. Im Punkt x=-0.37 ist f(x) konvex

b. Im Punkt x=-0.38 ist die Steigung der Tangente an f(x) kleiner 15.22

c. Im Punkt x=0.08 ist f(x) steigend

d. Im Punkt x=-0.31 ist die zweite Ableitung von f(x) negativ

e. Der Punkt x=-0.76 ist ein stationärer Punkt von f(x)

Comments

Soll es eventuell \(-5x^3\cdot\) heißen?

---

Ja, hab nicht gesehn das es nicht lesbar angeschrieben wurde, sry!

---

Ok, ich habe es geändert.

---

Gehe ich recht in der Annahme, dass die fünf Aussagen anhand der Ergebnisse der Kurvendiskussion überprüft und nicht direkt nachgerechnet werden sollen?

---

Vom Duplikat:

Titel: Kurvendiskussion, Funktion

Stichworte: kurvendiskussion,funktion,ableitung

Gegeben ist die Funktion f(x)=-5 x 3 ·exp(-2x+4).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a. Im Punkt x=0.73 ist die zweite Ableitung von f(x) positiv b. Im Punkt x=0.51 ist die erste Ableitung von f(x) gleich -50.70 c. Der Punkt x=2.46 ist ein stationärer Punkt von f(x) d. Im Punkt x=2.63 ist f(x) konkav e. Im Punkt x=1.95 ist f(x) fallend

Danke für die Hilfe

---

EDIT: Hallo Jasmin. Das sind zwar andere Zahlen. Aber Rechenwege und Diskussionen findest du hier bereits.

---

Vom Duplikat:

Titel: Kurvendiskussion f(x)=3 x^2 ·exp(2.5x+5).

Stichworte: kurvendiskussion,konvex,steigend,minimum

Kann mir bei dieser Aufgabe vielleicht jemand helfen?

Gegeben ist die Funktion f(x)=3 x^2 ·exp(2.5x+5).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a. Im Punkt x=-0.66 ist f(x) konvex

b. Im Punkt x=-0.35 ist f(x) steigend

c. Der Punkt x=0.00 ist ein lokales Maximum von f(x)

d. Im Punkt x=-0.93 ist die zweite Ableitung von f(x) negativ

e. Im Punkt x=-0.64 ist die Steigung der Tangente an f(x) gleich -23.01

---

Schau mal hier: https://www.mathelounge.de/480551/kurvendiskussion-von-f-x-5x-3%C2%B7exp-4x-5

---

Danke Lu für die Hilfe.

würde der Ansatz so stimmen?

Gegeben ist die Funktion f(x)=-5 x 3 ·exp(-2x+4).
Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a. Im Punkt x=0.73 ist die zweite Ableitung von f(x) positiv
b. Im Punkt x=0.51 ist die erste Ableitung von f(x) gleich -50.70
c. Der Punkt x=2.46 ist ein stationärer Punkt von f(x)
d. Im Punkt x=2.63 ist f(x) konkav e. Im Punkt x=1.95 ist f(x) fallend

erste Ableitung: 5x²(2x-3)e^4-2x

x=3/2 ≈1,5

also ist b) falsch?

zweite Ableitung x= -√3-3/2 =0,6339

also ist a) auch falsch?

Danke für die Hilfe :)

---

@Jasmin: 

" erste Ableitung: f ' (x) =  5x²(2x-3)e^4-2x 

x=3/2 =1,5  "

Hier hast du eine Nullstelle der ersten Ableitung bestimmt (Falls die 1. Ableitung stimmt). D.h. die Stelle x = 3/2 ist möglicherweise eine Extremalstelle. 

Eine zweite Nullstelle der 1. Ableitung ist x = 0. 

Weitere Stellen mit horizontaler Tangente gibt es dann nicht. D.h. das Einzige, was du damit sagen kannst, ist dass c) falsch ist.

Um etwas zu b. und e. sagen zu können, musst du bei der ersten Ableitung das angegebene x einsetzen und f'(x) ausrechnen.

---

Vom Duplikat:

Titel: Kurvensdiskussion von f(x) = -1x^3 · exp ( -3x + 4)

Stichworte: kurvendiskussion,konvex,stationärer,punkt

Gegeben ist die Funktion

f (x) = -1x^3 · exp ( -3x + 4)

Führen Sie eine Kurvendiskussion durch und kreuzen Sie alle richtigen Aussagen an.

a) Im punkt x= 1.43 ist f (x) konvex

b) im punkt x=1.69 ist f (x) fallend

c)der punkt x= 1.00 ist ein stationärer punkt von f (x)

d) im punkt x= 1.23 ist die Steigung der Tangente an f (x) kleiner als 1.42

e) im punkt x= 0.03 ist die zweite ableitung von f (x) negativ

---

https://www.mathelounge.de/schreibregeln Wähle bitte aussagekräftigere Überschriften und vermeide Duplikate. Rubrik "ähnliche Fragen" Bsp. https://www.mathelounge.de/480551/kurvendiskussion-von-f-x-5x-3%C2%B7exp-4x-5 

Versuche mal das zu übertragen und melde dich mit deinen Ansätzen, Skizzen und Rechnungen in einem Kommentar, falls du unsicher bist.

---

Hallo Lu,

in den letzten Tagen sind mehrere Fragen
exakt der gleichen Art wie diese hier gestellt
worden.
Irgendetwas stimmt doch da nicht.
Ebenso sind für die Ölfirma Schnell
mehrere Fragen der gleichen Art gestellt
worden.
ich denke hier will uns jemand auf den
Arm nehmen.

Ich denke hier trollt jemand.

mfg Georg

---

Ich beantworte diese Fragen nicht mehr und verweise auf vorhandene Antworten. Die haben personalisierte Aufgaben. Gelegentlich stellen sie tatsächlich eine Rechnung ein und die sollte man dann korrigieren. Lass es bitte mal bei einer Meldung pro Frage bewenden, damit die Frage nicht ausgeblendet wird und wir die Überschriften, Links und Tags nochmals neu eingeben müssen und / oder vrohandene Rechnungen verschwinden.

Das Problem ist vor allem, dass die neuen Fragen und ecthe Lösungsversuche untergehen.

Answer 1

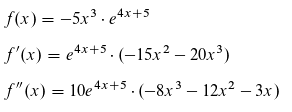
a) Im Punkt x=-0.37 ist f(x) konvex 

Voraussetzunng dafür ist, dass f ''(-0,37) > 0, das ist hier nicht der Fall, denn f''(-0,37) = -43,1

b) Im Punkt x=-0.38 ist die Steigung der Tangente an f(x) kleiner 15.22

f'(-0,38) = -34,9, also nicht 15,22

c) Im Punkt x=0.08 ist f(x) steigend

f'(0,08) = -21,71 = fallend

d) Im Punkt x=-0.31 ist die zweite Ableitung von f(x) negativ

f''(-0,31) = 6,45, also falsch

e)
Der Punkt x=-0.76 ist ein stationärer Punkt von f(x)

Bedingung: f'(-0,76) 0 0 und f''(-0,76)

f'(-0,76) = 0,82, also kein stationärer Punkt

Bei Fragen bitte melden.

Answer 2

Stimmt deine Funktionsangabe ?
1. Zeile Funktion
2. Zeile 1.Ableitung
3. Zeile 2.Ableitung

Bin bei Bedarf weiter behilflich.