Hallo bluup! :-)
Am Einfachsten geht es wohl, wenn Du die Graphen ohne eine Wertetabelle zeichnest.
Zeichne den Graphen von y = 2x - 3 im positiven y-Bereich. Im negativen y-Bereich brauchen wir den Graphen nicht, darum ist der lediglich gestrichelt angedeutet.
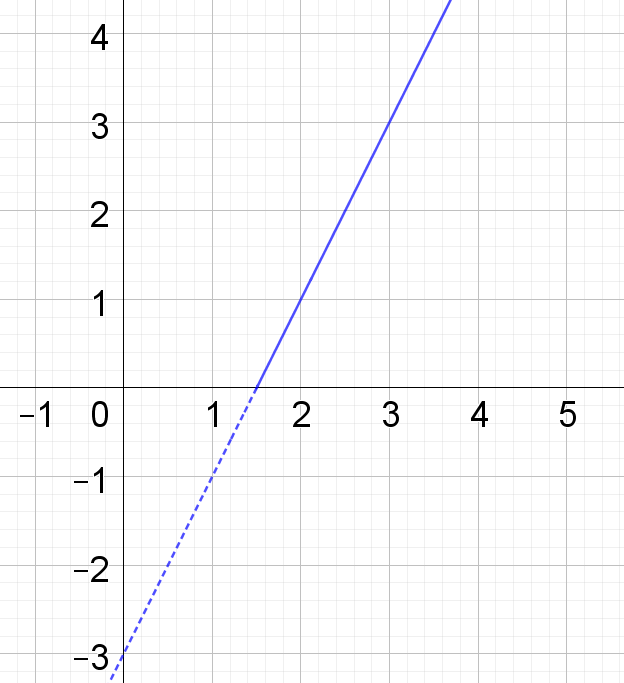
Spiegle den gestrichelten, negativen y-Bereich des Graphen an der x-Achse. Fertig ist der Graph von y = |2x - 3|.
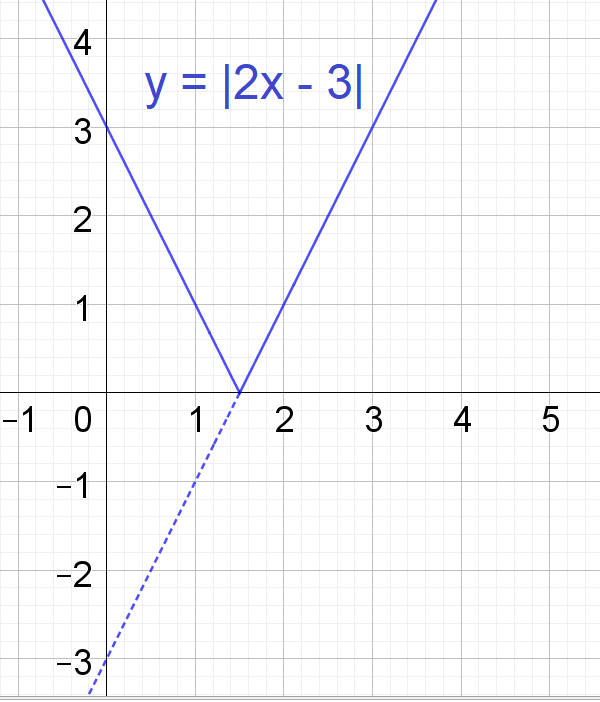
Zeichne die Gerade y = 5. Schraffiere den Bereich |2x - 3| ≤ 5.
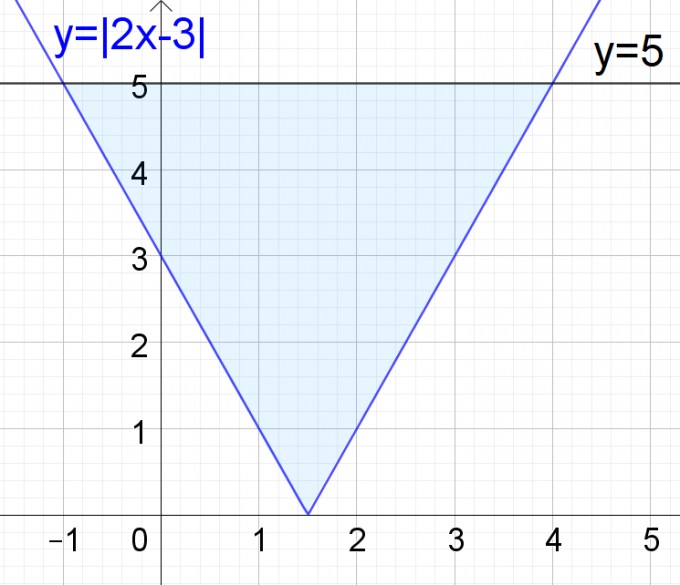
Das gleiche in grün machst Du nun mit |2x + 1| >3. Zeichne also den Graphen von |2x + 1|. Zeichne y = 3. Schraffiere den Bereich |2x + 1| > 3.
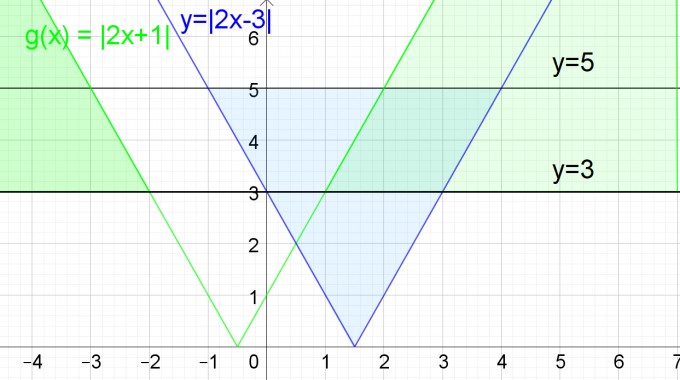
Der überlappte Bereich hervorgehoben:
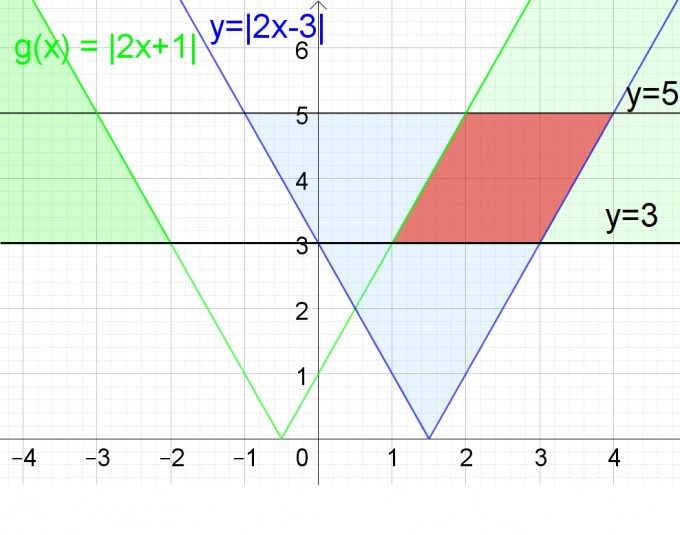
Die Lösungsmenge L lässt sich ablesen:
Für x > 1 ist |2x + 1| > 3 und für x ≤ 4 ist |2x - 3| ≤ 5. Wir erhalten L = {x ∈ ℝ| 1 < x ≤ 4}. D.h. für 1 < x ≤ 4 gilt |2x - 3| ≤ 5 und |2x + 1| > 3.
Beste Grüße
gorgar