S steht senkrecht über E, wenn das Skalarprodukt beider Vektoren null ergibt, also
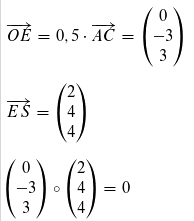
Die Höhe der Pyramide ergibt sich aus der Länge des Vektors ES = 6
Die Seite a der Grundfläche ist ebenfalls 6.
Somit ist das Volumen
$$ V= \frac{1}{3}·6^2 · 6 = 72 $$