Funktionenscharen - Zeigen sie rechnerisch

Question

unzwar komme ich mit folgender Aufgabe nicht klar

( es handelt sich um Funktionenscharen)

Gegeben ist die Funktionenschar f^a mit f^a(x) = x^2 - ax^3 + 1 (a ungleich 0).

a) Zeigen Sie rechnerisch, dass alle Graphen von f^a einen Wendepunkt haben.

b) Zeigen sie rechnerisch, dass die Wendepunkte der Schar alle auf einer Parabel liegen und bestimmen sie die zugehörige Gleichung. 

Answer 1

Hallo mala,

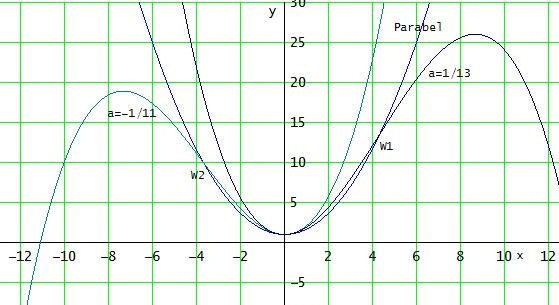
a)

f_a(x)  =  x² - ax³ + 1 

f_a'(x)  = 2·x - 3·a·x²

f_a"(x)  =  2 - 6·a·x  =  0    →   x_a = 1 / (3a)  mit VZW von f "  →  Wendestelle

 f_a( 1 / (3a) )  =  1 / (9a² )  -  a · 1 / (27a³) + 1 = 3 / (27a³) - 1 / (27a³)  =  2 / (27·a²) + 1   

             →    Wendepunkt (  1 / (3a) |  2 / (27·a²) + 1 )

b)

x = 1 / (3a)  →  a = 1 / (3x)

a in y-Wert einsetzen:

y  = 2 / (27·a²) + 1  = 2/3 · x²  + 1 

ist die gesuchte Parabel, auf der alle Wendepunkte liegen.

Gruß Wolfgang